tìm m để phương trình x4 + mx2 - m - 1 = 0 có 4 nghiệm phân biệt
x4-mx2+m-1 =0 .Biết m= m0 là giá trị để phương trình có 4 nghiệm phân biệt trong đó hai nghiệm dương thỏa mãn |x1-x2|=1 . Tìm m0
\(x^4-1-mx^2+m=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)-m\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=m-1\end{matrix}\right.\)
Pt có 4 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ne2\end{matrix}\right.\)
Khi đó ta có:
\(\left|x_1-x_2\right|=\left|1-\sqrt{m-1}\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{m-1}=1\\1-\sqrt{m-1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=5\end{matrix}\right.\)
Vậy \(m_0=5\)
Cho phương trình x 4 + m x 2 + 2 m + 3 = 0 (1). Với giá trị nào dưới đây của m thì phương trình (1) có 4 nghiệm phân biệt?
A. m = - 7 5
B. m = −1
C. m = - 3 2
D. m = 4 - 2 7
Cho phương trình x4 - 2( m+1 )x2 + 2m+1 = 0
Tìm m để phương trình có 4 nghiệm phân biệt
Đặt \(x^2=t\left(t\ge0\right)\), phương trình trở thành:
\(t^2-2\left(m+1\right)t+2m+1=0\left(1\right)\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2>0\\t_1+t_2=2m+2>0\\t_1t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m\ne0\end{matrix}\right.\)
Tìm m để phương trình m - 1 x 4 - m x 2 + m 2 - 1 = 0 có ba nghiệm phân biệt.
A. m = ±1.
B. m = 1.
C. m = −1.
D. m = 0.
+ Khi m - 1 = 0 ⇔ m = 1 phương trình cho trở thành: - x 2 = 0 ⇔ x = 0
Do đó: m = 1 không thỏa mãn đề bài.
+ Khi m - 1 ≠ 0 ⇔ m ≠ 1
Đặt t = x 2 t ≥ 0
Phương trình cho trở thành m - 1 t 2 - m t + m 2 - 1 = 0 1
Phương trình cho có ba nghiệm phân biệt ⇔ 1 có hai nghiệm t 1 , t 2 thoả t 1 = 0 < t 2
Khi t 1 = 0 ⇒ m = ± 1 . Do có hai nghiệm phân biệt nên m ≠ 1
Với m = - 1 ⇒ t 2 = 1 2 (nhận).
Đáp án cần chọn là: C
Tìm tất cả các giá trị của tham số m để phương trình x 2 - m x 2 + 1 + m + 4 = 0 có bốn nghiệm phân biệt
A. m>6
B. m>4
C. m>7
D. m>5
Tìm m để phương trình
mx2+(2m-1)x+m-2=0 có 2 nghiệm phân biệt đều âm
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\\Delta=\left(2m-1\right)^2-4m\left(m-2\right)>0\\x_1+x_2=\dfrac{1-2m}{m}< 0\\x_1x_2=\dfrac{m-2}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\4m+1>0\\\dfrac{1-2m}{m}< 0\\\dfrac{m-2}{m}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{4}\\\left[{}\begin{matrix}m< 0\\m>\dfrac{1}{2}\end{matrix}\right.\\\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{4}< m< 0\\m>2\end{matrix}\right.\)
1) Cho phương trình x 4 + m x 2 - m - 1 = 0(m là tham số)
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
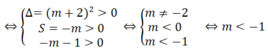
Tìm tất cả các nghiệm thực của tham số m để phương trình mx2 + 2(m + 1)x + m = 0 có hai nghiệm phân biệt.
A. m ≠ 0 m > - 1 2
B. m > 1 2
C. m > - 1 2
D. m > 0
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 4 nghiệm phân biệt

Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
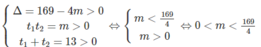
Tìm tất cả các nghiệm thực của tham số m để phương trình m x 2 + 2 m + 1 x + m = 0 có hai nghiệm phân biệt.
A. m ≠ m > - 1 2
B. m > 1 2
C. m > - 1 2
D. m > 0