Ai giải hộ mik với
Xét sự biến thiên của hàm số
Y=X^2
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
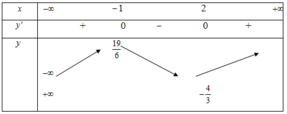
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Đáp án là D.
• Sai ở bước III (bảng biến thiên)
Xét sự biến thiên của hàm số y=
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
a) y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
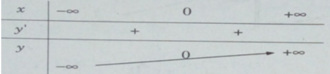
Đồ thị:
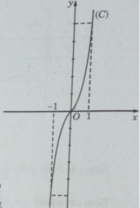
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì f′(x0) = 12 x 0 2 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x0 = 1 hoặc x0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
c) Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔ 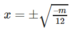
Từ đó suy ra:
y’ > 0 với

y’ < 0 với
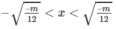
Vậy hàm số (1) đồng biến trên các khoảng
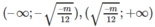
và nghịch biến trên khoảng
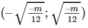
Xét sự biến thiên của hàm số y=\(\frac{2}{3-x}\) trên khoảng (3;+ vô cực)
x>3
nên 3-x<0
=>Hàm số nghịch biến khi x>3
Xét sự biến thiên của hàm số y = 3 x − 1 trên khoảng (1; + ∞ )
A. Đồng biến
B. Nghịch biến
C. Vừa đồng biến, vừa nghịch biến
D. Không đồng biến, cũng không nghịch biến
Cho hàm số \(y=\sqrt{x-1}+x^2-2x\)
a, Xét sự biến thiên của hàm số đã cho trên [ 1;+\(\infty\))
b, Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn \(\left[2;5\right]\)
please help me
i need it now
Xét sự biến thiên của hàm số
\(a.y=-2x^2+x+1\\ b.y=\sqrt{2-x}\\ c.y=\sqrt{2x-x^2}\)
a. Với $x_1, x_2\in\mathbb{R}$ thỏa $x_1\neq x_2$ thì:
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{-2(x_1^2-x_2^2)+(x_1-x_2)}{x_1-x_2}=1-2(x_1+x_2)\)
Với $x_1,x_2> \frac{1}{4}$ thì $A< 0$ nên hàm số nghịch biến trên $(\frac{1}{4}; +\infty)$
Với $x_1,x_2< \frac{1}{4}$ thì $A>0$ nên hàm số đồng biến trên $(-\infty; \frac{1}{4})$
b. TXĐ: $D=(-\infty; 2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2-x_1}-\sqrt{2-x_2}}{x_1-x_2}=\frac{-1}{\sqrt{2-x_1}+\sqrt{2-x_2}}< 0\)
Vậy hàm số nghịch biến trên tập xác định $(-\infty;2]$
c. TXĐ: $D=[0;2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2x_1-x_1^2}-\sqrt{2x_2-x_2^2}}{x_1-x_2}=\frac{2-(x_1+x_2)}{\sqrt{2x_1-x_1^2}+\sqrt{2x_2-x_2^2}}\)
Nếu $x_1,x_2\in (1;2)$ thì $A<0$ nên hàm số nghịch biến trên $(1;2)$
Nếu $x_1,x_2\in (0;1)$ thì $A>0$ nên hàm số nghịch biến trên $(0;1)$
Xét sự biến thiên và vẽ đồ thị của hàm số y=|-3x+3|
(giúp em với mọi người ,gấp lắm ạ)
hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)