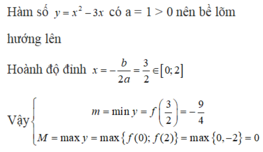tìm giá trị nhỏ nhất x2+3x+3

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của
A = x2 + x + 5
B = x2 - 3x + 2
\(A=x^2+x+5=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
Dấu "=" xảy ra khi \(x=-\dfrac{1}{2}\)
\(B=x^2-3x+2=\left(x-\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu "=" xảy ra khi \(x=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của
a) B = x2 – 4x + 6
b) C = x2 – 3x – 1
a: Ta có: \(B=x^2-4x+6\)
\(=x^2-4x+4+2\)
\(=\left(x-2\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
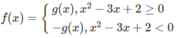
nên ta có đồ thị f(x) như sau:
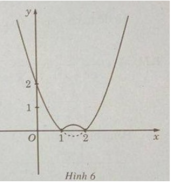
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
Đúng 0
Bình luận (0)
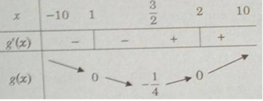
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
y
f
(
x
)
x
2
−
3
x
trên đoạn [0;2] A.
M
0
;
m
−
9
4
B.
M
9
4
;
m
0
C.
M
−
2...
Đọc tiếp
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f ( x ) = x 2 − 3 x trên đoạn [0;2]
A. M = 0 ; m = − 9 4
B. M = 9 4 ; m = 0
C. M = − 2 , m = − 9 4
D. M = 2 , m = − 9 4
Bài 1: Tìm giá trị nhỏ nhất của các biểu thứca ) A x2 – 2x+5b) B x2 –x +1c) C ( x -1). ( x +2). ( x+3). ( x+6)d) D x2 + 5y2 – 2xy+ 4y+3Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:a) A -x2 – 4x – 2 b) B -2x2 – 3x +5c) C ( 2- x). ( x +4)d) D -8x2 + 4xy - y2 +3Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biếna) A 25x – 20x+7b) B 9x2 – 6xy + 2y2 +1c) E x2 – 2x + y2 + 4y+6d) D x2 – 2x +2Giúp mình nha. Cần gấp ạ Chi tiết nha
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất của các biểu thức
a ) A= x2 – 2x+5
b) B= x2 –x +1
c) C= ( x -1). ( x +2). ( x+3). ( x+6)
d) D= x2 + 5y2 – 2xy+ 4y+3
Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:
a) A= -x2 – 4x – 2
b) B= -2x2 – 3x +5
c) C= ( 2- x). ( x +4)
d) D= -8x2 + 4xy - y2 +3
Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biến
a) A= 25x – 20x+7
b) B= 9x2 – 6xy + 2y2 +1
c) E= x2 – 2x + y2 + 4y+6
d) D= x2 – 2x +2
Giúp mình nha. Cần gấp ạ <Chi tiết nha>
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức:
B= x2+3x-1
mk cần gấp !!!
\(B=x^2+3x-1=x^2+2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{13}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
\(B_{min}=\dfrac{-13}{4}\Leftrightarrow x=\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
g
x
x
2
+
3
x
với
x
∈
ℝ
. A.
-
9
4
B.
-
3
2
C. 0 D.
3
2
Đọc tiếp
Tìm giá trị nhỏ nhất của biểu thức g x = x 2 + 3 x với x ∈ ℝ .
A. - 9 4
B. - 3 2
C. 0
D. 3 2
Ta có: x 2 ≥ 0 ; 3 x ≥ 0 ∀ x ⇒ g x = x 2 + 3 x ≥ 0 ∀ x
Do đó, giá trị nhỏ nhất của biểu thức g(x) là 0 khi x= 0.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
2
+
3
x
-
1
trên đoạn [2;4].
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 2 + 3 x - 1 trên đoạn [2;4].
![]()
![]()
![]()
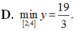
Tìm giá trị nhỏ nhất của hàm số
y
x
2
+
3
x
−
1
trên đoạn [2;4] A.
min
2
;
4
y
−
2
B.
min...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 2 + 3 x − 1 trên đoạn [2;4]
A. min 2 ; 4 y = − 2
B. min 2 ; 4 y = 6
C. min 2 ; 4 y = 19 3
D. min 2 ; 4 y = − 3
Đáp án B
Ta có y ' = x 2 − 2 x − 3 x − 1 2 ⇒ y ' = 0 ⇔ x = − 1 x = 3
Suy ra y 2 = 7 , y 3 = 6 , y 4 = 19 3 ⇒ min 2 ; 4 y = 6
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
2
+
3
x
-
1
trên đoạn [2;4] A.
m
i
n
2
;
4
y
6
B. ...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 2 + 3 x - 1 trên đoạn [2;4]
A. m i n 2 ; 4 y = 6
B. m i n 2 ; 4 y = - 2
C. m i n 2 ; 4 y = - 3
D. m i n 2 ; 4 y = 19 3