Cho tam giác ABC vuông tại A, đường cao AH = \(\dfrac{\sqrt{6}}{3}\), đường trung tuyến CM =

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, biết , BC = 10 cm .
a)Giải tam giác vuông ABC ?
b)Vẽ đường cao AH, đường trung tuyến AM . Tính độ dài AH, HM?
a, \(\tan B=\dfrac{4}{3}\Leftrightarrow\dfrac{AC}{AB}=\dfrac{4}{3}\Leftrightarrow AC=\dfrac{4}{3}AB\)
Áp dụng PTG: \(AB^2+AC^2=AB^2+\dfrac{16}{9}AB^2=\dfrac{25}{9}AB^2=BC^2=100\)
\(\Leftrightarrow AB^2=36\Leftrightarrow AB=6\left(cm\right)\\ \Leftrightarrow AC=6\cdot\dfrac{4}{3}=8\left(cm\right)\)
\(\tan B=\dfrac{4}{3}\approx\tan53^0\Leftrightarrow\widehat{B}\approx53^0\\ \widehat{C}=90^0-\widehat{B}\approx90^0-53^0=37^0\)
b, Vì AM là trung tuyến ứng ch BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{48}{10}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH = \(\dfrac{\sqrt{6}}{3}\), đường trung tuyến CM = \(\dfrac{3}{2}\) AB. Tính AB, AC, BC
Cho tam giác ABC vuông tại A đường cao AH Đường trung tuyến AM
a) Hãy chỉ ta các điểm là trọng tâm ,trực tâm giữa 3 đường trung trực của tam giác ABC
b) cho AB=16 cm AC=12 cm Tính AH;AM;MH
Câu 9. Cho tam giác ABC vuông tại A, đường cao AH, phân giác AD, trung tuyến AM. Biết AB = 6 cm, AM = 5cm. Độ dài AH, BH, HM là
Gấp !!!
BC=2*AM=10cm
AC=căn 10^2-6^2=8cm
AH=6*8/10=4,8cm
BH=AB^2/BC=6^2/10=3,6cm
MH=căn 5^2-4,8^2=1,4cm
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có chu vi 72 cm, trung tuyến AM, hiệu trung tuyến AM và đường cao AH=7cm. Tính diện tích tam giác ABC
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Cho tam giác ABC vuông tại A , đường cao AH , trung tuyến AM .Biết AH =4 cm , AM = 4,1 cm . Tỉ số độ dài 2 canh goc vuông AB và AC của tam giác ABC = ?
cho tam giác ABC vuông tại A, biết AB=3cm; AC=4cm. Kẻ đường cao AH và trung tuyến AM. CM tam giác AHB và tam giác ABC đồng dạng
Xét \(\Delta ABC\&\Delta ABH\) ta có:
\(\widehat{A}=\widehat{B}=90^o\left(gt\right)\\ \widehat{B}=\widehat{B}\\\Rightarrow \Delta ABC\&\sim ABH\)
Đúng 2
Bình luận (2)
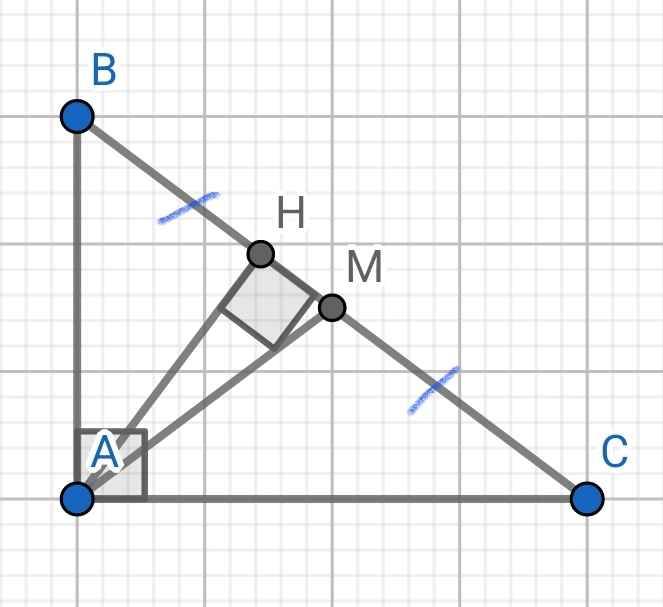
Xét ∆AHB và ∆CBA có:
∠AHB = ∠CAB = 90⁰
∠B chung
⇒ ∆AHB ∽ ∆CBA (g-g)
Đúng 1
Bình luận (0)
Xét ΔABC&ΔABH ta có:
góc A= góc B= 90 độ (gt)
góc B= góc B
⇒ΔABC&∼ABH
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc kẻ từ H đến AB, AC
a) cm: EF = AH
b) kẻ trung tuyến của tam giác ABC. Cm: AM vuông góc với EF




















