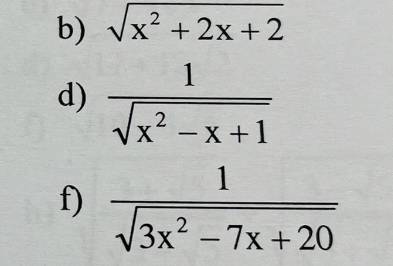
b: ĐKXĐ: x^2+2x+2>=0

=>(x+1)^2+1>=0(luôn đúng)

d: ĐKXĐ: x^2-x+1>0

=>(x-1/2)^2+3/4>0(luôn đúng)

f: ĐKXĐ: 3x^2-7x+20>0

=>x^2-7/3x+20/3>0

=>x^2-2*x*7/6+49/36+191/36>0

=>(x-7/6)^2+191/36>0(luôn đúng)

Đề không rõ. Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

\(a,ĐK:x>0;x\ne1;x\ne4\\ b,P=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\\ P=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{3}=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)

\(\sqrt{1-x}\)

ĐKXĐ:\(1-x\ge0\Rightarrow x\le1\)

\(\sqrt{x-1}\)

ĐKXĐ:\(x-1\ge0\Rightarrow x\ge1\)

\(\sqrt{1-x}xđ< =>1-x>0< =>-x>-1< =>x< 1\)
\(\sqrt{x-1}xđ< =>x-1>0< =>x>1\)

ĐKXĐ: \(x\le-\dfrac{5}{2}\)

ĐKXĐ: \(x+1>0\Rightarrow x>-1\)

Để một biểu thức có nghĩa thì mẫu số phải khác 0.

\(\Rightarrow a^2+3a-4\ne0\)

Nếu \(a^2+3a-4=0\)thì:

\(a^2+3a-4=a^2-a+4a-4\)

\(=a\left(a-1\right)+4\left(a-1\right)=\left(a-1\right)\left(a+4\right)=0\)

\(\Rightarrow\)a - 1 = 0 hoặc a + 4 = 0

\(\Rightarrow\)a = 1 hoặc a = -4

Vậy để biểu thức có nghĩa thì a khác 1 và -4.
 

\(\sqrt{x^2-x+1}\) có nghĩa khi \(x^2-x+1\ge0\)

Ta có \(x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Với mọi x, ta có \(\left(x-\dfrac{1}{2}\right)^2\ge0\)    

\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)  (vì 3/4 > 0)

Do đó \(x^2-x+1>0\) với mọi x

Vậy với bất cứ giá trị nào của x thì căn thức trên xác định.

ĐKXĐ: `x\inRR`

Vì `x^2-x+1=(x^2-x+1/4)+3/4=(x-1/2)^2+3/4>0AAx`