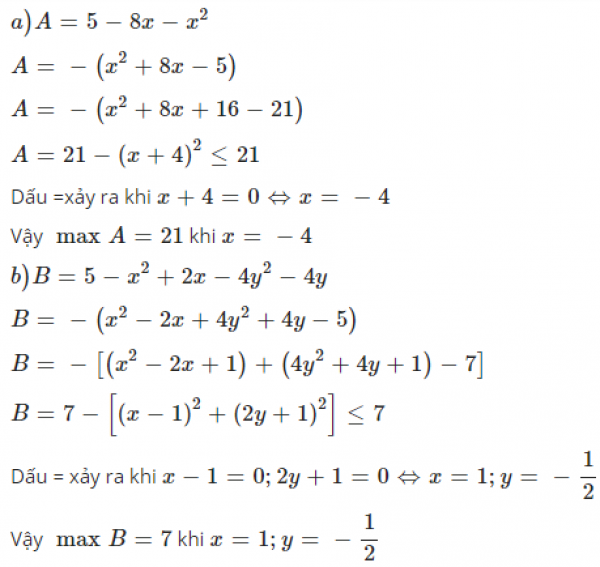a, \(A=-\left(x^2+8x+16-16\right)+5=-\left(x+4\right)^2+21\le21\forall x\)

Dấu ''='' xảy ra khi x = - 4

Vậy GTLN của A là 21 tại x = -4 

b, \(B=-\left(x^2-2x+1\right)-\left(4y^2+4y+1\right)+7\)

\(=-\left(x-1\right)^2-\left(2y+1\right)^2+7\le7\forall x;y\)

Dấu ''='' xảy ra khi x = 1 ; y = -1/2 

Vậy GTLN của B là 7 tại x = 1 ; y = -1/2 

TK

A = 5 − 8 x − x 2

= -(x2+8x+16)+21

= 21-(x+4)2 

Với mọi x thì ( x + 4 ) 2 >= 0

=> 21−(x+4)2=<21 Hay A=<21

Để A=21 thì (x+4)2=0

=>x+4=0

=> x = − 4

Câu sau để anh nghĩ đã nhé

`a)x^2-2x+2+4y^2+4y`

`=x^2-2x+1+4y^2+4y+1`

`=(x-1)^2+(2y+1)^2`

`b)4x^2+y^2+12x+4y+13`

`=4x^2+12x+9+y^2+4y+4`

`=(2x+3)^2+(y+2)^2`

`c)x^2+17+4y^2+8x+4y`

`=x^2+8x+16+4y^2+4y+1`

`=(x+4)^2+(2y+1)^2`

`d)4x^2-12xy+y^2-4y+13`

`=4x^2-12x+9+y^2-4y+4`

`=(2x-3)^2+(y-2)^2`

a) \(x^2-2x+2+4y^2+4y=\left(x-1\right)^2+\left(2y+1\right)^2\)

b) \(4x^2+y^2+12x+4y+13=\left(2x+3\right)^2+\left(y+2\right)^2\)

c) \(x^2+17+4y^2+8x+4y=\left(x+4\right)^2+\left(2y+1\right)^2\)

d) \(4x^2-12x+y^2-4y+13=\left(2x-3\right)^2+\left(y-2\right)^2\)

a: \(x^2-2x+2+4y^2+4y\)

\(=x^2-2x+1+4y^2+4y+1\)

\(=\left(x-1\right)^2+\left(2y+1\right)^2\)

b: \(4x^2+12x+y^2+4y+13\)

\(=4x^2+12x+9+y^2+4y+4\)

\(=\left(2x+3\right)^2+\left(y+2\right)^2\)

c: \(x^2+8x+4y^2+4y+17\)

\(=x^2+8x+16+4y^2+4y+1\)

\(=\left(x+4\right)^2+\left(2y+1\right)^2\)

d: \(4x^2-12x+y^2-4y+13\)

\(=4x^2-12x+9+y^2-4y+4\)

\(=\left(2x-3\right)^2+\left(y-2\right)^2\)

A= -x²+2x+3

=>A= -(x²-2x+3)

=>A= -(x²-2.x.1+1+3-1)

=>A=-[(x-1)²+2]

=>A= -(x+1)²-2

Vì -(x+1)² ≤0=> A≤-2

Dấu "=" xảy ra khi

-(x+1)²=0 => x=-1

Vây A lớn nhất= -2 khi x= -1

B=x²-2x+4y²-4y+8

=> B= (x²-2x+1)+(4y²-4y+1)+6

=> B=(x-1)²+(2y+1)²+6

=> B lớn nhất=6 khi x=1 và y=-1/2

Lời giải:

a)

$A=5-8x-x^2=21-(x^2+8x+16)=21-(x+4)^2$Vì $(x+4)^2\geq 0$ nên $A=21-(x+4)^2\leq 21$

Vậy GTLN của $A$ là $21$. Giá trị này đạt tại $x+4=0\Leftrightarrow x=-4$

b) 

$B=5-x^2+2x-4y^2-4y=5-(x^2-2x)-(4y^2+4y)$

$=7-(x^2-2x+1)-(4y^2+4y+1)$

$=7-(x-1)^2-(2y+1)^2$

Vì $(x-1)^2\geq 0; (2y+1)^2\geq 0$ với mọi $x,y$ nên $B=7-(x-1)^2-(2y+1)^2\leq 7$Vậy GTLN của $B$ là $7$ tại $x=1; y=\frac{-1}{2}$

a: Ta có: \(A=x^2-2xy+5y^2+4y+51\)

\(=x^2-2xy+y^2+4y^2+4y+1+50\)

\(=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\forall x,y\)

Dấu '=' xảy ra khi \(x=y=-\dfrac{1}{2}\)

a) \(A=x^2-2xy+5y^2+4y+51=\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)+50=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\)

\(minA=50\Leftrightarrow x=y=-\dfrac{1}{2}\)

c) \(C=\dfrac{9}{-2x^2+4x-7}=\dfrac{9}{-2\left(x^2-2x+1\right)-5}=\dfrac{9}{-2\left(x-1\right)^2-5}\ge\dfrac{9}{-5}=-\dfrac{9}{5}\)

\(minC=-\dfrac{9}{5}\Leftrightarrow x=1\)

d) \(10x^2+4y^2-4xy+8x-4y+20=\left[4y^2-4y\left(x+1\right)+\left(x+1\right)^2\right]+\left(9x^2+6x+1\right)+18=\left(2y-x-1\right)^2+\left(3x+1\right)^2+18\ge18\)

\(minD=18\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

e) \(E=9x^2+2y^2+6xy-6x-8y+10=\left[9x^2+6x\left(y-1\right)+\left(y-1\right)^2\right]+\left(y^2-6x+9\right)=\left(3x+y-1\right)^2+\left(y-3\right)^2\ge0\)

\(minE=0\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=3\end{matrix}\right.\)

$A=x^2+y^2-6x+4y+20=(x^2-6x+9)+(y^2+4y+4)+7$

$=(x-3)^2+(y+2)^2+7\geq 0+0+7=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x-3)^2=(y+2)^2=0$

$\Leftrightarrow x=3; y=-2$

---------------------

$B=9x^2+y^2+2z^2-18x+4z-6y+30$

$=(9x^2-18x+9)+(y^2-6y+9)+(2z^2+4z+2)+10$

$=9(x^2-2x+1)+(y^2-6y+9)+2(z^2+2z+1)+10$

$=9(x-1)^2+(y-3)^2+2(z+1)^2+10\geq 10$
Vậy $B_{\min}=10$. Giá trị này đạt tại $(x-1)^2=(y-3)^2=(z+1)^2$

$\Leftrightarrow x=1; y=3; z=-1$

$C=x^2+y^2+z^2-xy-yz-xz+3$

$2C=2x^2+2y^2+2z^2-2xy-2yz-2xz+6$

$=(x^2-2xy+y^2)+(y^2-2yz+z^2)+(x^2-2xz+z^2)+6$

$=(x-y)^2+(y-z)^2+(z-x)^2+6\geq 6$

$\Rightarrow C\geq 3$

Vậy $C_{\min}=3$. Giá trị này đạt tại $x-y=y-z=z-x=0$

$\Leftrihgtarrow x=y=z$

--------------------------------------

$D=5x^2+2y^2+4xy-2x+4y+2021$

$=2(y^2+2xy+x^2)+3x^2-2x+4y+2021$

$=2(x+y)^2+4(x+y)+3x^2-6x+2021$
$=2(x+y)^2+4(x+y)+2+3(x^2-2x+1)+2016$

$=2[(x+y)^2+2(x+y)+1]+3(x^2-2x+1)+2016$

$=2(x+y+1)^2+3(x-1)^2+2016\geq 2016$

Vậy $D_{\min}=2016$ khi $x+y+1=x-1=0$

$\Leftrightarrow x=1; y=-2$

$E=x^2-2x+4y^2+4y+2014$

$=(x^2-2x+1)+(4y^2+4y+1)+2012$

$=(x-1)^2+(2y+1)^2+2012$

$\geq 2012$

Vậy $E_{\min}=2012$. Giá trị này đạt tại $x-1=2y+1=0$

$\Leftrightarrow x=1; y=\frac{-1}{2}$

----------------------

$F=5x^2+5y^2+8xy+2y-2x+30$

$=4(x^2+2xy+y^2)+x^2+y^2+2y-2x+30$

$=4(x+y)^2+(x^2-2x+1)+(y^2+2y+1)+28$

$=4(x+y)^2+(x-1)^2+(y+1)^2+28\geq 28$

Vậy $F_{\min}=28$. Giá trị này đạt tại $x+y=x-1=y+1=0$

$\Leftrightarrow x=1; y=-1$