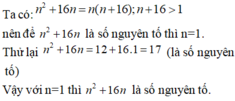Tìm các số tự nhiên n sao cho n2 16n 2011 là 1 số chính phương

Những câu hỏi liên quan
_Tìm các số tự nhiên n sao cho: n2 + 16n + 2011 là 1 số chính phương
Đặt \(n^2+16n+2011=k^2\left(k\in N\right)\)
\(< =>\left(n^2+16n+64\right)+1947=k^2\)
\(< =>\left(n+8\right)^2+1947=k^2< =>k^2-\left(n+8\right)^2=1947\)
\(< =>\left(k-n-8\right)\left(k+n+8\right)=1947\)
Có \(k-n-8< k+n+8\)
\(=>\left(k-n-8\right)\left(k+n+8\right)=1.1947=3.649=11.177\)
bn tự giải tiếp nhé,đến đây dễ rồi
Đúng 0
Bình luận (0)
_bạn còn thiếu 1 trường hợp là 59 .33 nhé # CTV Hoàng Phúc
Đúng 0
Bình luận (0)
uk , tks , bn tự bổ sung ,mk k có máy tính nên k chắc chắn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho số tự nhiên an=3n2+16n+13(n\(\in N\)).Tìm các số tự nhiên n sao cho an là số chính phương
2. Tìm các số tự nhiên n thoả mãn n2 +3n+2 là số nguyên tố.
3. Tìm các số tự nhiên n sao cho 2n +34 là số chính phương.
4. Chứng minh rằng tổng S = 14 +24 +34 +···+1004 không là số chính phương.
5. Tìm các số nguyên dương a ≤ b ≤ c thoả mãn abc,a+b+c,a+b+c+2 đều là các số nguyên tố
Mik gấp
đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
Đúng 1
Bình luận (0)
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP
Đúng 1
Bình luận (0)
2: A=n^2+3n+2=(n+1)(n+2)
Để A là số nguyên tố thì n+1=1 hoặc n+2=2
=>n=0
Đúng 0
Bình luận (0)
Tìm tất cả các số tự nhiên n để n 2 + 16 n là số nguyên tố.
A. n=11
B. n=17
C. n=1
D. n=15
1.Cho biểu thức:A=(a^2015+b^2015+c^2015)-(a^2011+b^2011+c^2011) với a,b,c là các số nguyên dương. Chứng minh rằng A chia hết cho 30
2. Tìm tất cả các số tự nhiên n sao cho n²-14n-256 là một số chính phương.
giúp mình với các bạn nhé!
CMR nếu n là số tự nhiên sao cho n+1 và n2+1 đều là các số chính phương thì n là bội của số 24
Giải cụ thể, chính xác cho mình nhé! ^^
Vì 2n+1 là số chính phương lẻ nên
2n+1≡1(mod8)⇒2n⋮8⇒n⋮42n+1≡1(mod8)⇒2n⋮8⇒n⋮4
Do đó n+1 cũng là số lẻ, suy ra
n+1≡1(mod8)⇒n⋮8n+1≡1(mod8)⇒n⋮8
Lại có
(n+1)+(2n+1)=3n+2(n+1)+(2n+1)=3n+2
Ta thấy
3n+2≡2(mod3)3n+2≡2(mod3)
Suy ra
(n+1)+(2n+1)≡2(mod3)(n+1)+(2n+1)≡2(mod3)
Mà n+1 và 2n+1 là các số chính phương lẻ nên
n+1≡2n+1≡1(mod3)n+1≡2n+1≡1(mod3)
Do đó
n⋮3n⋮3
Vậy ta có đpcm.
Đúng 0
Bình luận (0)
Bài 1: tìm tất cả các số tự nhiên n thoả mãn
b) n2 - n + 1 là số chính phương
Tìm các số tự nhiên n sao cho n! +14 là số chính phương
Tìm cá số tự nhiên n sao cho n! + 19 là số chính phương
Số tự nhiên n sao cho n2 + 404 là số chính phương
Các bạn giúp mình giải cụ thể nhé!