bài tập :
cho đường thẳng (d) y=mx+2(m#0)
đường thẳng (d) cắt Ox tại b tìm m sao cho
a, tam giác OAB vuông cân tịa O
b, diện tích OAB bằng 3
c, khoảng cách từ O đến dường thẳng (d) bằng 1
Những câu hỏi liên quan
Bài 16: Cho 3 đường thẳng: (d_{1}) : y = 2x + 3 ; (d_{2}) d,): y = - x + 4 ;(d ): y = mx + m - 1 a. Vẽ hai đường thẳng (d_{1}); (d_{2}) trên cùng 1 mặt phẳng tọa độ. b. Tính góc tạo bởi đường thẳng (d_{1}) với trục Ox (làm tròn đến phút). c. Tìm m để 3 đường thăng trên đồng quy.
b: tan a=2
nên a=63 độ
c: Tọa độ giao của (d1) và (d2) là:
2x+3=-x+4 và y=2x+3
=>x=1/3 và y=2/3+3=8/3
Thay x=1/3 và y=8/3 vào (d3), ta được:
1/3m+m-1=8/3
=>4/3m=11/3
=>m=11/3:4/3=11/3*3/4=11/4
Đúng 0
Bình luận (0)
Bài 2: Cho đường thẳng d: y = mx + 2m + 1 và d’: y = - x (m là tham số)
a)Tìm điểm cố định mà họ đường thẳng d luôn đi qua với mọi m.
b) Tìm m để khoảng cách từ gốc tọa độ O đến d là lớn nhất.
c) Tìm m để d// d’. Với m tìm được hãy vẽ đường thẳng d. Giả sử d cắt trục Ox, Oy lần lượt tại A và B. Tính diện tích tam giác OAB và khoảng cách từ O tới d.
20 tháng 4 2023 lúc 6:34
Cho parabol (P): \(y=\dfrac{x^2}{2}\) và đường thẳng (d): \(y=mx+\dfrac{1}{2}\)
a) C/M (d) luôn đi qua điểm cố định
b) C/M (d) luôn cắt (P) tại 2 điểm M và N
c) Tìm tập hợp trung điểm I của đoạn thẳng MN
Dạ bày em câu (c) với ạ em không biết làm:"(
Pt hoành độ giao điểm (P) và (d):
\(\dfrac{x^2}{2}=mx+\dfrac{1}{2}\Leftrightarrow x^2-2mx-1=0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_M+x_N=2m\\x_Mx_N=-1\end{matrix}\right.\)
Gọi I là trung điểm MN \(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_M+x_N}{2}\\y_I=\dfrac{y_M+y_N}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{2m}{2}=m\\y_I=\dfrac{m.x_M+\dfrac{1}{2}+m.x_N+\dfrac{1}{2}}{2}=\dfrac{m\left(x_M+x_N\right)+1}{2}=m^2+\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow y_I=x_I^2+\dfrac{1}{2}\)
Hay tập hợp I là parabol có pt: \(y=x^2+\dfrac{1}{2}\)
Đúng 2
Bình luận (6)
Cho hai đường thẳng d: y = x + 2m, d′: y = 3x + 2 (m là tham số). Tìm m để ba đường thẳng d, d′ và d′′: y = −mx + 2 phân biệt đồng quy.
A. m = −1
B. m = 3
C. m = 1
D. m = −3
cho đường thẳng (d): y = mx + 2 m Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng
(d)là căn 2
Để tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2, ta sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
Đường thẳng (d) có phương trình y = mx + 2. Khoảng cách từ gốc tọa độ đến đường thẳng (d) được tính bằng công thức:
d = |Ax + By + C| / căn(A^2 + B^2)
Với A, B, C lần lượt là hệ số của x, y và số hạng tự do trong phương trình đường thẳng.
Trong trường hợp này, A = -m, B = 1, C = -2. Và khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2.
Vậy ta có phương trình:
|0 - m*0 - 2| / căn((-m)^2 + 1^2) = căn 2
|0 - 2| / căn(m^2 + 1) = căn 2
| - 2| / căn(m^2 + 1) = căn 2
2 / căn(m^2 + 1) = căn 2
Bình phương cả hai vế của phương trình:
4 / (m^2 + 1) = 2
4 = 2(m^2 + 1)
4 = 2m^2 + 2
2m^2 = 2
m^2 = 1
m = ±1
Vậy, để khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2, ta có hai giá trị của m: 1 và -1.
Đúng 0
Bình luận (0)
cho đường thẳng (d):y=mx+2.giá trị của m để đường thẳng d tiếp xúc với đường kính bán kính 1.
Bài 5. (1 điểm) Cho parabol (P): y = −𝑥 ^2 và đường thẳng (d): y = mx − 1.
1. Chứng minh với mọi giá trị của m đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B.
2. Gọi 𝑥1 , 𝑥2 là hai hoành độ của A, B. Tìm m sao cho 𝑥1 ^3 + 𝑥2^ 3 = − 4.
1) Phương trình hoành độ giao điểm của (P) và (d) là:
\(-x^2=mx-1\)
\(\Leftrightarrow-x^2-mx+1=0\)
a=-1; b=-m; c=1
Vì ac<0 nên (P) luôn cắt (d) tại hai điểm phân biệt với mọi m
Đúng 1
Bình luận (0)
2) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-m\right)}{-1}=-m\\x_1x_2=\dfrac{c}{a}=\dfrac{1}{-1}=-1\end{matrix}\right.\)
Ta có: \(x_1^3+x_2^3=-4\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+4=0\)
\(\Leftrightarrow\left(-m\right)^3-3\cdot\left(-1\right)\cdot\left(-m\right)+4=0\)
\(\Leftrightarrow-m^3-3m+4=0\)
\(\Leftrightarrow m^3+3m-4=0\)
\(\Leftrightarrow m^3-m+4m-4=0\)
\(\Leftrightarrow m\left(m-1\right)\left(m+1\right)+4\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m+4\right)=0\)
\(\Leftrightarrow m-1=0\)
hay m=1
Đúng 0
Bình luận (0)
Cho hai đường thẳng d: y= x+ 2m và d’: y= 3x+2 ( m là tham số). Có mấy giá trị của m để ba đường thẳng d; d’ và d’’: y= -mx+ 2 phân biệt đồng quy.
A.0
B. 1
C. 2
D. 3
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
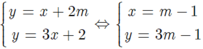
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
Đúng 0
Bình luận (0)
Bài 2: (2,0 điểm) Cho (P): y = 1/2x ^ 2 và đường thẳng (d): y = mx + 2
a) Chứng tỏ rằng (d) cắt (P) tại hai điểm phân biệt A và B.
b) Xác định m để AB có độ dài ngắn nhất
a: PTHĐGĐ là;
1/2x^2-mx-2=0
a=1/2; b=-m; c=-2
Vì a*c<0 nên (d) luôn cắt (P) tại hai điểm phân biệt
Đúng 0
Bình luận (0)
Cho (P): y=x^2 và đường thẳng (d): y=mx-1 (m là tham số) .Để đường thẳng (d) cắt (P) tại 2 điểm phân biệt thì m nhận giá trị là:
Phương trình hoành độ giao điểm là:
\(x^2-mx+1=0\)
\(\text{Δ}=m^2-4\)
Để (P) cắt (d) tại hai điểm phân biệt thì (m-2)(m+2)>0
=>m>2 hoặc m<-2
Đúng 1
Bình luận (0)