cho tứ giác lồi abcd,gọi m,n là trung điểm ab,cd.cmr:2mn=ad+bc giúp em với ạaa

Những câu hỏi liên quan
Cho tứ giác lồi ABCD, gọi M,N là trung điểm AB, CD. CMR 2MN ≤ AB+BC
Cho tứ giác lồi ABCD. Gọi M,N,P,Q,E,F lần lượt là trung điểm của AB , CD, AD, BD, AC. BC CMR: MN, PQ, EF đồng quy.
Ta có : Tứ giác MPNQ là hình bình hành
MN và PQ cắt nhau tại trung điểm I của mỗi đường
Ta có : Tứ giác EPFQ là hình bình hành
EF đi qua I
Vậy EF , MN và PQ đồng quy
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:
AB
→
+
C
D
→
A
D
→
+
C
B...
Đọc tiếp
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng: AB → + C D → = A D → + C B → = 2 M N →
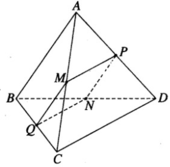
Ta có MPNQ là hình bình hành vì

Do đó
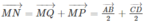
hay 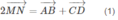
Mặt khác 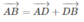
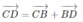
Nên
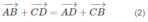
Vì

Từ (1) và (2) ta có:
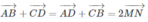
là đẳng thức cần chứng minh
Đúng 1
Bình luận (0)
Cho tứ giác lồi ABCD có AB = CD góc A bằng 70 độ góc C bằng 50 độ Gọi M N lần lượt là trung điểm của BC và AD Tính góc ANM
Cho tứ giác lồi ABCD , hai cạnh đối AD và BC bằng nhau. Gọi M,N,P,Q theo thứ tự là trung điểm của AC , BD, AB và DC . CMR PQ là trung trực của MN
Cho tứ giác ABCD,gọi M,N lần lượt là trung điểm các cạnh BC và CD.CMR SABCD < 1/2(AM+AN)2
GIÚP MK VS
Cho hbh ABCD. Gọi I, K lần lượt là trung điểm của BC, AD a, cm tứ giác ABIK là hbh b, gọi M là giao điểm của AI và BK, N là giao điểm của CK và DI. Chứng minh BC=2MN c, Khi AC=BD và AB=3cm,BC=4cm.Tính diện tích hbh ABCD d, cm AN,DM,IK cùng đi qua 1 điểm G và tính độ dài GK với độ dài AB,BC đã cho ở trên
Cho tứ giác ABCD có AD = BC. Gọi E, F, M, N lần lượt là trung điểm AB, CD, BD, AC. Chứng minh tứ giác EMFN là hình thoi. mn giúp mik với plsss![]()
![]()
Xét ΔABC có
E là trung điểm của AB
N là trung điểm của AC
Do đó: EN là đường trung bình của ΔABC
Suy ra: EN//BC và \(EN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
M là trung điểm của BD
F là trung điểm của CD
Do đó: MF là đường trung bình của ΔBDC
Suy ra: MF//BC và \(MF=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABD có
E là trung điểm của AB
M là trung điểm của BD
Do đó: EM là đường trung bình của ΔABD
Suy ra: \(EM=\dfrac{AD}{2}=\dfrac{BC}{2}\left(3\right)\)
Từ (1) và (2) suy ra EN//MF và EN=MF
Từ (1) và (3) suy ra EN=EM
Xét tứ giác ENFM có
EN//MF
EN=MF
Do đó: ENFM là hình bình hành
mà EN=EM
nên ENFM là hình thoi
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD. Gọi M, N, E, F theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác MNEF là hình gì? Vì sao?
Bạn tra gu gồ được mà,hỏi làm gì cho mệt chớ,tìm được cách làm trên gu gồ là áp dụng vào bài thôi
Đúng 0
Bình luận (0)
noi A vs C ,BvsC
ap dung tinh chat duong trug binh cua tam giac
AM=EN
MN=FE
MNEF la hinh thoi
Đúng 0
Bình luận (0)
















