Giúp mình với: \(\dfrac{x-2}{4}=\dfrac{5+x}{3}\)

Những câu hỏi liên quan
5x - 4 > 2x - 5
<=> 5x - 2x > 5 + 4
<=> 3x > 9
<=> x > \(\dfrac{9}{3}\)
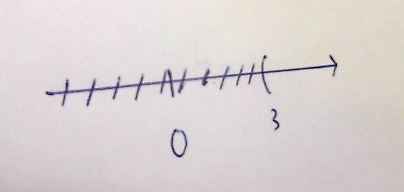
<=> x > 3
Ai chỉ giúp mình kết luận với biểu diễn tập nghiệm trên trục số đi
\(\dfrac{x+1}{60}\)+\(\dfrac{x+2}{59}\)=\(\dfrac{x+3}{58}\)+\(\dfrac{x+4}{57}\)
Mọi người giúp mình với!!!
\(\dfrac{x+1}{60}+\dfrac{x+2}{59}=\dfrac{x+3}{58}+\dfrac{x+4}{57}\)
\(\Leftrightarrow\dfrac{x+1}{60}+1+\dfrac{x+2}{59}+1=\dfrac{x+3}{58}+1+\dfrac{x+4}{57}+1\)
\(\Leftrightarrow\dfrac{x+1+60}{60}+\dfrac{x+2+59}{59}=\dfrac{x+3+58}{58}+\dfrac{x+4+57}{57}\)
\(\Leftrightarrow\dfrac{x+61}{60}+\dfrac{x+61}{59}-\dfrac{x+61}{58}-\dfrac{x+61}{57}=0\)
\(\Leftrightarrow\left(x+61\right)\left(\dfrac{1}{60}+\dfrac{1}{59}-\dfrac{1}{58}-\dfrac{1}{57}\right)=0\)
\(\Leftrightarrow x+61=0\)
\(\Leftrightarrow x=-61\)
Đúng 0
Bình luận (0)
y= \(\dfrac{1}{3}\)\(x^3\)+(m+1)\(x^2\)+(m+3)x+2m
m=? hàm số đồng biến trong (0,1);(2,∞)
Giúp mình với ! please ..
Thực hiện phép tính
a) (x\(^2\)-3x+4)(-3x+1)
b)\(\dfrac{1}{x}\)+\(\dfrac{1}{x+5}\)+\(\dfrac{x-5}{x^2+5x}\)
Mọi người giúp mình nhanh nha mình cần gấp
b: \(=\dfrac{x+5+x+x-5}{x\left(x+5\right)}=\dfrac{3x}{x\left(x+5\right)}=\dfrac{3}{x+5}\)
Đúng 1
Bình luận (0)
\(a,=-3x^3+x^2+9x^2-3x-12x+4=-3x^3+10x^2-15x+4\\ b,=\dfrac{x+5+x+x-5}{x\left(x+5\right)}=\dfrac{3x}{x\left(x+5\right)}=\dfrac{3}{x+5}\)
Đúng 2
Bình luận (1)
y= \(\dfrac{1}{3}\)\(x^3\)+\(\dfrac{1}{2}\)(m-1)\(x^2\)+(2m-1)x-1
a, m=? đồng biến trên R
b, m=? đồng biến trên ( -∞ , -2) và ( 0 ,1)
Giúp mình với ! Please T-T
y'=1/3*3x^2+1/2*2x(m-1)+(2m-1)
=x^2+x(m-1)+2m-1
a: y đồng biến trên R thì y'>0 với mọi x thuộc R
Δ=(m-1)^2-4(2m-1)
=m^2-2m+1-8m+4=m^2-10m+5
Để y'>0 với mọi x thuộc R thì m^2-10m+5<0
=>5-2*căn 5<m<5+2căn 5
b: y đồng biến trên (-vô cực;-2) và (0;1) khi y'>0 với mọi x thuộc (-vô cực;-2) và (0;1)
y'=x^2+x(m-1)+2m-1
=x^2+xm-x+2m-1
=m(x+2)+x^2-x-1
y'>0 với x thuộc (-vô cực;-2)
=>m>-x^2+x+1/(x+2) với x thuộc (vô cực;-2)
g(x)=-x^2+x+1/(x+2)
g'=(-x^2+x+1)'(x+2)-(-x^2+x+1)(x+2)'/(x+2)^2
=(x+2+x^2-x-1)/(x+2)^2=(x^2+1)/(x+2)^2>0 với mọi x
=>m thuộc (-vô cực;-2)
Tương tự, ta cũng được: m thuộc (0;1)
Đúng 1
Bình luận (0)
Cho biểu thức
\(A=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
a) tìm điều kiện xác định rồi rút gọn biểu thức A
b) tìm giá trị của x để A>0
c) tính giá trị của A trong trườn hợp \(|x-7|=4\)
LÀM ƠN GIÚP GIÚP GIÚP MÌNH VỚI MÌNH CẦN GẤP LẮM LUN
B1: Giải các phương trình sau
1) left(3x-2right)left(dfrac{2left(x+3right)}{7}-dfrac{4x-3}{5}right)0
2) left(x-dfrac{3}{4}right)^2+left(x-dfrac{3}{4}right)left(x-dfrac{1}{2}right)0
3) dfrac{12}{9-x^2}+dfrac{2}{x-3}+dfrac{3}{x+3}1
4) dfrac{1}{x-1}+dfrac{2}{x^2+x+1}dfrac{3x^2}{x^3-1}
các bạn ơi giúp mình với
mik cảm ơn !!!
Đọc tiếp
B1: Giải các phương trình sau
1) \(\left(3x-2\right)\left(\dfrac{2\left(x+3\right)}{7}-\dfrac{4x-3}{5}\right)=0\)
2) \(\left(x-\dfrac{3}{4}\right)^2+\left(x-\dfrac{3}{4}\right)\left(x-\dfrac{1}{2}\right)=0\)
3) \(\dfrac{12}{9-x^2}+\dfrac{2}{x-3}+\dfrac{3}{x+3}=1\)
4) \(\dfrac{1}{x-1}+\dfrac{2}{x^2+x+1}=\dfrac{3x^2}{x^3-1}\)
các bạn ơi giúp mình với
mik cảm ơn !!!
I : tìm x
a) (x-1)(x-5)>0
b) (x-1)(x-5)<0
c) \(\dfrac{3}{4}-\dfrac{1}{4}\left|x-\dfrac{1}{7}\right|=\dfrac{1}{4}\)
d) \(\left(x-\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)
e) 8 (x+1) -2(2x+5)=0
g) ( 6x-1)-(x+8)=0
h)\(\left|7x-\dfrac{1}{4}\right|=1\)
q) -2x-3=-x+7
các bạn giúp mình với xin đó đấy
\(\text{a) }\left(x-1\right)\left(x-5\right)>0\\ \text{ Để }\left(x-1\right)\left(x-5\right)>0\text{ thì }\Rightarrow x-1\text{ và }x-5\text{ cùng dấu }\\ \text{+) Xét }x-1\text{ và }x-5\text{ là số nguyên dương }\Rightarrow\left\{{}\begin{matrix}x-1>0\Rightarrow x>1\\x-5>0\Rightarrow x>5\end{matrix}\right.\Rightarrow x>5\\ \text{+) Xét }x-1\text{ và }x-5\text{ là số nguyên âm }\Rightarrow\left\{{}\begin{matrix}x-1< 0\Rightarrow x< 1\\x-5< 0\Rightarrow x< 5\end{matrix}\right.\Rightarrow x< 1\\ \text{Vậy }\left(x-1\right)\left(x-5\right)>0\text{ khi }x< 1\text{ hoặc }x>5\)
\(\text{b) }\left(x-1\right)\left(x-5\right)< 0\\ \text{ Để }\left(x-1\right)\left(x-5\right)< 0\text{ thì }\Rightarrow x-1\text{ và }x-5\text{ trái dấu }\\ \text{ Mà }x-1>x-5\\ \Rightarrow\left\{{}\begin{matrix}x-1>0\Rightarrow x>1\\x-5< 0\Rightarrow x< 5\end{matrix}\right.\Rightarrow1< x< 5\\ \text{ Vậy }\left(x-1\right)\left(x-5\right)< 0\text{ khi }1< x< 5\)
Đúng 0
Bình luận (0)
\(\text{c) }\dfrac{3}{4}-\dfrac{1}{4}\left|x-\dfrac{1}{7}\right|=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{4}\left|x-\dfrac{1}{7}\right|=\dfrac{1}{2}\\ \Leftrightarrow\left|x-\dfrac{1}{7}\right|=2\\ \Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{7}=-2\\x-\dfrac{1}{7}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{13}{7}\\x=\dfrac{15}{7}\end{matrix}\right.\\ \text{Vậy }x=-\dfrac{13}{7}\text{ hoặc }x=\dfrac{15}{7}\)
\(\text{d) }\left(x-\dfrac{1}{2}\right)^2=\dfrac{1}{16}\\ \Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=-\dfrac{1}{4}\\x-\dfrac{1}{2}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\\ \text{Vậy }x=\dfrac{1}{4}\text{ hoặc }x=\dfrac{3}{4}\)
\(\text{e) }8\left(x+1\right)-2\left(2x+5\right)=0\\ \Leftrightarrow8x+8-4x+10=0\\ \Leftrightarrow\left(8x-4x\right)+\left(8+10\right)=0\\ \Leftrightarrow4x+18=0\\ \Leftrightarrow4x=-18\\ \Leftrightarrow x=-\dfrac{9}{2}\\ \text{Vậy }x=-\dfrac{9}{2}\)
\(\text{g) }\left(6x-1\right)-\left(x+8\right)=0\\ \Leftrightarrow6x-1-x-8=0\\ \Leftrightarrow\left(6x-x\right)-\left(1+8\right)=0\\ \Leftrightarrow5x-9=0\\ \Leftrightarrow5x=9\\ \Leftrightarrow x=\dfrac{9}{5}\\ \text{Vậy }x=\dfrac{9}{5}\)
\(\text{h) }\left|7x-\dfrac{1}{4}\right|=1\\ \Leftrightarrow\left[{}\begin{matrix}7x-\dfrac{1}{4}=-1\\7x-\dfrac{1}{4}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}7x=-\dfrac{3}{4}\\7x=\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{28}\\x=\dfrac{5}{28}\end{matrix}\right.\\ \text{Vậy }x=-\dfrac{3}{28}\text{ hoặc }x=\dfrac{5}{28}\)
\(\text{q) }-2x-3=-x+7\\ \Leftrightarrow-2x-3-\left(-x+7\right)=0\\ \Leftrightarrow-2x-3+x-7=0\\ \Leftrightarrow\left(-2x+x\right)-\left(3+7\right)=0\\ \Leftrightarrow-x-10=0\\ \Leftrightarrow-x=10\\ \Leftrightarrow x=-10\\ \text{ Vậy }x=-10\)
Đúng 0
Bình luận (0)
Tìm GTLN - GTNN: P = \(\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)
Giúp mình với nhé ~ Mình cần gấp lắm!
Đặt \(\sqrt{x}=t\ge0\)
\(P=\dfrac{4t}{3t^2-3t+3}\Rightarrow3Pt^2-\left(3P+4\right)t+3P=0\left(1\right)\)
Ta cần tìm P để (1) có ít nhất một nghiệm không âm
\(\Delta=\left(3P+4\right)^2-36P^2=\left(4-3P\right)\left(4+9P\right)\ge0\)
\(\Rightarrow\dfrac{-4}{9}\le P\le\dfrac{4}{3}\) (2)
Để (1) có 2 nghiệm đều âm \(\Rightarrow\left\{{}\begin{matrix}\dfrac{3P+4}{3P}< 0\\\dfrac{3P}{3P}>0\end{matrix}\right.\) \(\Rightarrow\dfrac{-4}{3}< P< 0\)
\(\Rightarrow\) để (1) có ít nhất 1 nghiệm không âm thì \(P\ge0\) hoặc \(P\le\dfrac{-4}{3}\) (3)
Kết hợp (2) với (3) ta được: \(0\le P\le\dfrac{4}{3}\)
Vậy \(P_{min}=0\) và \(P_{max}=\dfrac{4}{3}\)
Đúng 0
Bình luận (2)