Trả lời:

a, ( - x + 5 )² - 16 = ( - 2² ) . 5

=> ( - x + 5 )² - 16 = - 20

=> ( - x + 5 )² = - 20 + 16

=> ( - x + 5 )² = - 4 ( vô lí )

Vậy không tìm được x thỏa mãn đề bài.

b, 50 - ( 20 - x ) = - x - ( 45 - 85 )

=> 50 - 20 + x = - x - ( - 40 )

=> 30 + x = - x + 40

=> x + x = 40 - 30

=> 2x = 10

=> x = 10 : 2

=> x = 5

Vậy x = 5

Câu 6: B

Câu 7: A

\(P=x^2-2x+5=x^2-2x+1+4=\left(x-1\right)^2+4\)

Vì \(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+4\ge4\)

=>P_min=(x-1)²+4=4

<=>(x-1)²=0

<=>x-1=0

<=>x=1

Vậy P_min=4 khi x=1

----------------------------------------------------------

\(Q=2x^2-6x=2\left(x^2-3x\right)=2\left[x^2-2.x.\frac{3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{2}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)

Vì \(\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)

=>Q_min=\(2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}=-\frac{9}{2}\)

<=>\(2\left(x-\frac{3}{2}\right)^2=0\)

<=>\(\left(x-\frac{3}{2}\right)^2=0\)

<=>\(x-\frac{3}{2}=0\)

<=>\(x=\frac{3}{2}\)

Vậy Q_min=\(-\frac{9}{2}\) khi \(x=\frac{3}{2}\)

Cảm ơn bạn nha

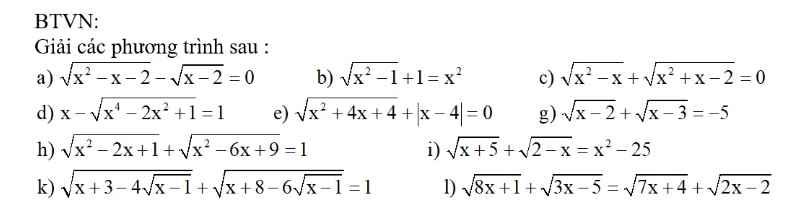
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)

\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)

\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)

\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)

\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{\left(x^2-1\right)^2}=x-1\\ \Leftrightarrow\left|x^2-1\right|=x-1\\ \Leftrightarrow\left[{}\begin{matrix}x^2-1=x-1\left(x\le-1;x\ge1\right)\\x^2-1=1-x\left(-1< x< 1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\\\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

\(e,PT\Leftrightarrow\left|x+2\right|+\left|x-4\right|=0\Leftrightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

\(g,\Leftrightarrow x\in\varnothing\left(\sqrt{x-2}+\sqrt{x-3}\ge0>-5\right)\\ f,\Leftrightarrow\left|x-1\right|+\left|x-3\right|=1\\ \Leftrightarrow\left[{}\begin{matrix}1-x+3-x=1\left(x< 1\right)\\x-1+3-x=1\left(1\le x< 3\right)\\x-1+x-3=1\left(x\ge3\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(ktm\right)\\0x=-1\left(ktm\right)\\x=\dfrac{5}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow x\in\varnothing\)

\(a,A=\left(\dfrac{x+14\sqrt{x}-5}{x-25}+\dfrac{\sqrt{x}}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+2}{\sqrt{x}-5}\)

\(\Rightarrow A=\left(\dfrac{x+14\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right).\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)

\(\Rightarrow A=\left(\dfrac{x+14\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{x-5\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right).\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)

\(\Rightarrow A=\dfrac{x+14\sqrt{x}-5+x-5\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)

\(\Rightarrow A=\dfrac{2x+9\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)

\(\Rightarrow A=\dfrac{2x+10\sqrt{x}-\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)

\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}+5\right)-\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)

\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)

\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+2}\)

câu hỏi đâu bn ?

bài đâu bn

rút gọn à banj

đúng rồi á

\(A=\dfrac{\left(x-\sqrt{2}\right)^2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}=\dfrac{x-\sqrt{2}}{x+\sqrt{2}}\)

\(B=\dfrac{x+\sqrt{5}}{\left(x+\sqrt{5}\right)^2}=\dfrac{1}{x+\sqrt{5}}\)