[Chuyên mục Fact meme]
Học nhiều rồi chúng ta cũng phải giải trí chứ nhỉ :D Dưới đây làm một sự thật nhiều bạn sử dụng khi làm IELTS Writting :)) Meme - Cuộc thi Trí tuệ VICE - Bài viết | Facebook

[Chuyên mục: Các tính chất + định lý hình học phẳng]
Nếu thích, hãy like bài viết ngay tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook

Ad ơi cho em hỏi cách chứng minh ạ. Và ví dụ như khi làm bài có cần chứng minh lại không ạ?
Bài chứng minh của Nguyễn Tiến Dũng: http://geometry-math-journal.ro/pdf/Volume6-Issue1/6.pdf
Bài chứng minh của Nguyễn Minh Hà: http://geometry-math-journal.ro/pdf/Volume6-Issue1/4.pdf
Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha!
(3-4 điểm thưởng/ý làm)

các bạn khác k làm thì đừng cmt vô đây mấy bài của các bạn giải bị trôi
1, \(\)BDT AM-GM
\(=>\sqrt{a^2+b^2}\ge\sqrt{2ab}\left(1\right)\)
tương tuqj \(=>\sqrt{b^2+c^2}\ge\sqrt{2bc}\left(2\right)\)
\(=>\sqrt{c^2+a^2}\ge\sqrt{2ac}\left(3\right)\)
cộng vế (1)(2)(3)
\(=>Vt=\sqrt{2}\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)=\sqrt{2021}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\dfrac{\sqrt{2021}}{\sqrt{2}}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\le a+b+c\)\(=>a+b+C\ge\dfrac{\sqrt{2021}}{\sqrt{2}}\)
đặt \(P=\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\)
\(=>P\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}=\dfrac{1}{2}.\dfrac{\sqrt{2021}}{\sqrt{2}}\)
dấu"=" xảy ra<=>\(a=b=c=\dfrac{\sqrt{2021}}{3\sqrt{2}}\)
Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha!

 (3-4 điểm thưởng/ý làm)
(3-4 điểm thưởng/ý làm)
C7, \(\dfrac{\left(b+c\right)\left(a^2+bc\right)}{b^2+bc+c^2}\ge\dfrac{\left(2\sqrt{bc}\right).\left(2a\sqrt{bc}\right)}{3\sqrt[3]{b^2.bc.c^2}}=\dfrac{4abc}{3abc}=\dfrac{4}{3}\left(1\right)\)
tương tự \(=>\dfrac{\left(a+c\right)\left(b^2+Ac\right)}{a^2+ac+c^2}\ge\dfrac{4}{3}\left(2\right)\)
\(=>\dfrac{\left(b+a\right)\left(c^2+ba\right)}{a^2+ab+b^2}\ge\dfrac{4}{3}\left(3\right)\)
cộng vế (1)(2)(3) \(=>P\ge4\)
dấu"=" xảy ra<=>a=b=c=1
ằng một đoạn văn khoảng 8 câu, em hãy trình bày cảm nhận của mình về nhân vật Mèo trong truyện Bức tranh của em gái tôi. Trong đoạn văn, có sử dụng một phép so sánh (yêu cầu gạch chân câu có phép so sánh đó và chú thích rõ)
Like page Facebook Cuộc thi Trí tuệ VICE ngay nha mọi người! Hãy giúp chúng mình đạt 10k likes! Link page: Cuộc thi Trí tuệ VICE | Facebook.
Câu hình, đề chuyên Toán Hải Phòng:

Sáng nay đề chuyên Nguyễn Huệ khó lắm ạ mình làm được mỗi câu a. :(
mới đọc đề thôi mà đã nát não *điên*
khó thật đấy ông ạ , Tôi và chắc dưới trung bình qúa:*((
Ai chưa xem thì nên xem thử nha, giàu cảm xúc lắm đấy :))
Bộ phim này lấy đi nước mắt của rất nhiều khán giả.
Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Hóa học.C17 _ 2.8.2021 | Cộng đồng giáo viên (Facebook) |


Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Toán.C17 _ 2.8.2021 | Nguyễn Minh Hoàng (Hoc24) |
| Toán.C18 _ 2.8.2021 | Trên con đường thành công không có dấu chân của kẻ lười biếng (Hoc24) |

| Ngữ văn.C19 _ 2.8.2021 | Ẩn danh (Hoc24) |
"Trong khoang thuyền, dàn nhạc gồm đàn tranh, đàn nguyệt, tì bà, nhị, đàn tam. Ngoài ra cũng có đàn bầu, sáo và cặp sanh để gõ nhịp" dùng để biểu diễn làn điệu nghệ thuật nào? Viết đoạn văn khoảng 10 câu nêu cảm nhận về vẻ đẹp của làn điệu ấy được giới thiệu trong văn bản. Trong đó có sử dụng câu văn dùng cụm chủ vị để mở rộng câu (gạch chân và chú thích rõ).
Đánh lại câu 17 dành cho ai thấy mờ quá:
CMR với \(n\ge6\), \(\sqrt{1+\dfrac{2.6.10...\left(4n-2\right)}{\left(n+5\right)\left(n+6\right)...2n}}\) là số nguyên dương.
C18:
\(A=a^3+b^3+c^3+3a^2+3b^2+3c^2\)'
\(=a^3+3a^2+2a+b^3+3b^2+2b+c^3+3c^2+2c-2\left(a+b+c\right)\)
\(=a\left(a+1\right)\left(a+2\right)+b\left(b+1\right)\left(b+2\right)+c\left(c+1\right)\left(c+2\right)-2\left(a+b+c\right)\)
Xét \(a\left(a+1\right)\left(a+2\right)\) là tích 3 số nguyên liên tiếp nên tích của chúng chia hết cho 6.
Lại có \(a+b+c⋮3\) nên \(2\left(a+b+c\right)⋮6\)
Từ đó suy ra \(A⋮6\) ( đpcm )
Câu C18 các anh chị nhường cho các bạn lớp 7, lớp 8 nhé.
Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Vật lí.C23 _ 2.8.2021 | Nguyễn Thanh Dương (Hoc24) |
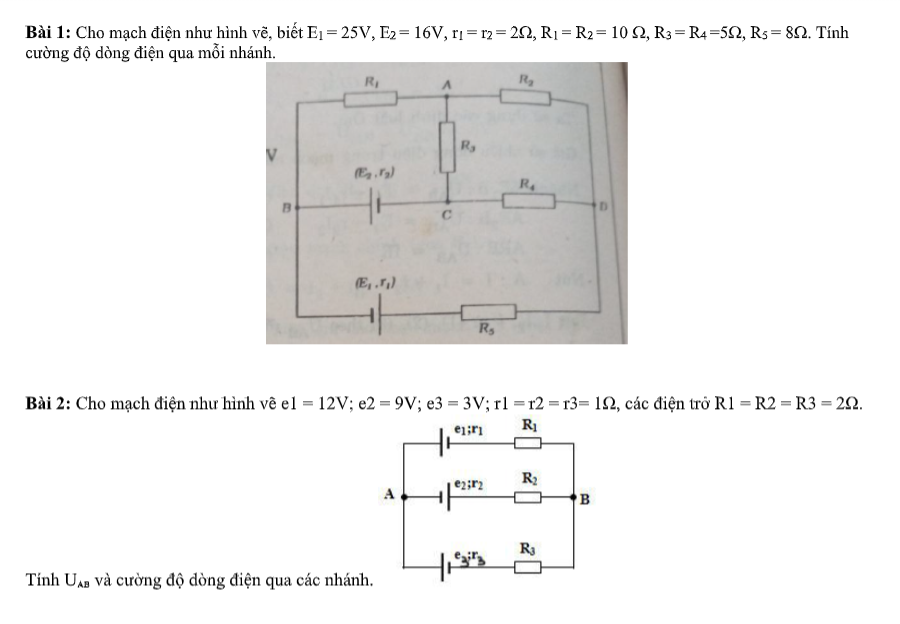

bài 2
cđ dđ
\(I_1=\dfrac{\xi_1}{r_1+R_1}=4\left(A\right)\)
\(I_2=\dfrac{\xi_2}{r_2+R_2}=3\left(A\right)\)
\(I_3=\dfrac{\xi_3}{r_3+R_3}=1\left(A\right)\)
\(U_{AB}=-\xi_2+I_2r_2=-6\left(V\right)\)
Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Toán.C27 _ 3.8.2021 | Rin Huỳnh (Hoc24) |



| Toán.C28 _ 3.8.2021 | Hir Dương (Hoc24) |
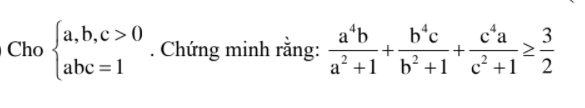
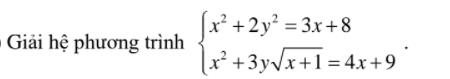
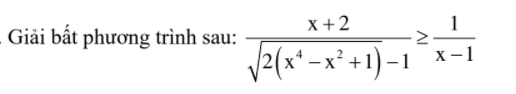

C27.1
Ta có: \(P=a^2+b^2+\dfrac{5}{a+b+1}=\left(a^2+1\right)+\left(b^2+1\right)+\dfrac{5}{a+b+ab+1+1}-2\)
\(\ge\dfrac{\left(a+1\right)^2}{2}+\dfrac{\left(b+1\right)^2}{2}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-2\)
\(\ge2\sqrt{\dfrac{\left(a+1\right)^2\left(b+1\right)^2}{4}}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-2\)
\(=\left(a+1\right)\left(b+1\right)+1+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-3\)
\(=\dfrac{\left(a+1\right)\left(b+1\right)+1}{5}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}+\dfrac{4\left(a+1\right)\left(b+1\right)+4}{5}-3\)
\(\ge2+\dfrac{4.2\sqrt{a}.2\sqrt{b}+4}{5}-3=2+\dfrac{4.4\sqrt{ab}+4}{5}-3=3\)
Dấu ''='' xảy ra khi và chỉ khi a=b=1
C28.1
Ta có VT=\(\dfrac{a^4b^2}{a^2b+b}+\dfrac{b^4c^2}{b^2c+c}+\dfrac{c^4a^2}{c^2a+a}\ge\dfrac{\left(a^2b+b^2c+c^2a\right)^2}{a^2b+b^2c+c^2a+a+b+c}\)
Vì \(\left(a^2b+b^2c+c^2a\right)^3\ge\left(a+b+c\right)^3\) ( Theo bđt holder)
\(\Leftrightarrow a^2b+b^2c+c^2a\ge a+b+c\)
\(\Rightarrow VT\ge\dfrac{\left(a^2b+b^2c+c^2a\right)^2}{2\left(a^2b+b^2c+c^2a\right)}=\dfrac{a^2b+b^2c+c^2a}{2}\ge\dfrac{3\sqrt[3]{\left(abc\right)^3}}{2}=\dfrac{3}{2}\)
Dấu ''='' xảy ra khi a=b=c