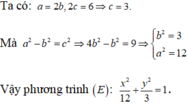Lập pt elip bt đọ dài trục lớn hơn trục nhỏ 4 đơn vị vs độ dài trục nhỏ hơn độ dài tiêu cự 4 đv

Những câu hỏi liên quan
Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị. A.
x
2
64
+
y
2
60
1.
B.
x
2
25
+
y
2
9
1....
Đọc tiếp
Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị.
A. x 2 64 + y 2 60 = 1.
B. x 2 25 + y 2 9 = 1.
C. x 2 100 + y 2 64 = 1.
D. x 2 9 + y 2 1 = 1.
Elip (E) có độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị nên 2a – 2b = 4 hay a – b = 2
Elip (E) có độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị nên 2b – 2c = 4 hay b – c = 2
Từ đó, ta có hệ phương trình:
a − b = 2 b − c = 2 a 2 = b 2 + c 2 ⇒ a − b = 2 c = b − 2 a 2 = b 2 + b − 2 2 ⇔ a = b + 2 c = b − 2 b + 2 2 = 2 b 2 − 4 b + 4 ⇔ a = b + 2 c = b − 2 b 2 − 8 b = 0 ⇒ a = 10 b = 8 c = 6
Phương trình chính tắc của Elip là E : x 2 100 + y 2 64 = 1
Đáp án C
Đúng 0
Bình luận (0)
lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục bé 4 đơn vị ,độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị
Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng
2
, tổng bình phương độ dài trục lớn và tiêu cự bằng 64. A.
x
2
12
+
y
2
8
1.
B.
x
2
8
+
y
2...
Đọc tiếp
Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng 2 , tổng bình phương độ dài trục lớn và tiêu cự bằng 64.
A. x 2 12 + y 2 8 = 1.
B. x 2 8 + y 2 12 = 1.
C. x 2 12 + y 2 4 = 1.
D. x 2 8 + y 2 4 = 1.
Elip (E) có tỉ số độ dài trục nhỏ và tiêu cự bằng 2 ⇒ 2 b 2 c = 2 ⇒ c = b 2 2 .
Mặt khác, 2 a 2 + 2 c 2 = 64 ⇔ a 2 + c 2 = 16 .
Ta có
c = b 2 2 a 2 + c 2 = 16 a 2 = b 2 + c 2 ⇒ a 2 + 1 2 b 2 = 16 a 2 − 3 2 b 2 = 0 ⇔ a 2 = 12 b 2 = 8
Phương trình chính tắc của Elip là E : x 2 12 + y 2 8 = 1 .
Chọn A.
Đúng 0
Bình luận (0)
Lập phương trình chính tắc của elip biết :
a) Độ dài trục lớn và trục nhỏ lần lượt là 8 và 6
b) Độ dài trục lớn bằng 10 và tiêu cự bằng 6
Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 - 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1.
Đúng 0
Bình luận (0)
Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:
a) Đỉnh \((5;0),(0;4)\)
b) Đỉnh \((5;0)\), tiêu điểm \((3;0)\)
c) Độ dài trục lớn 16, độ dài trục nhỏ 12
d) Độ dài trục lớn 20, tiêu cự 12
a) Từ giả thiết ta có \(a = 5,b = 4\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
b) Ta có: \(a = 5,c = 3 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
c) Từ giả thiết ta có: \(2a = 16,2b = 12 \Rightarrow a = 8,b = 6\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)
d) Từ giả thiết ta có: \(2a = 20,2c = 12 \Rightarrow a = 10,c = 6 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
Đúng 0
Bình luận (0)
Phương trình chính tắc của elip có độ dài trục lớn bằng hai lần độ dài trục nhỏ và tiêu cự bằng 6 là: A.
x
2
64
+
y
2
36
1
B.
x
2
12
+
y
2...
Đọc tiếp
Phương trình chính tắc của elip có độ dài trục lớn bằng hai lần độ dài trục nhỏ và tiêu cự bằng 6 là:
A. x 2 64 + y 2 36 = 1
B. x 2 12 + y 2 3 = 1
C. x 2 9 + y 2 12 = 1
D. 9 x 2 + 12 y 2 = 108
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)? A.
x
2
12
-
y
2
3
1
B.
x
2
12
+
y
2...
Đọc tiếp
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)?
A. x 2 12 - y 2 3 = 1
B. x 2 12 + y 2 3 = 1
C. x 2 3 + y 2 12 = 1
D. x 2 48 + y 2 12 = 1
Lập phương trình chính tắc của elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng
1
3
A.
x
2
9
+
y
2
8
1.
B.
x
2
9
+
y
2
5...
Đọc tiếp
Lập phương trình chính tắc của elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng 1 3
A. x 2 9 + y 2 8 = 1.
B. x 2 9 + y 2 5 = 1.
C. x 2 6 + y 2 5 = 1.
D. x 2 9 + y 2 3 = 1.
Elip (E) có độ dài trục lớn bằng 6 nên 2a= 6 hay a= 3.
Elip (E) có tỉ số của tiêu cự với độ dài trục lớn bằng 1 3
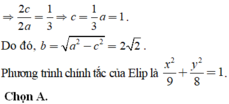
Đúng 0
Bình luận (0)
Lập phương trình chính tắc của elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục lớn bằng 12/13 A.
x
2
26
+
y
2
25
1.
B.
x
2
169
+
y
2
25
1.
C. ...
Đọc tiếp
Lập phương trình chính tắc của elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục lớn bằng 12/13
A. x 2 26 + y 2 25 = 1.
B. x 2 169 + y 2 25 = 1.
C. x 2 52 + y 2 25 = 1.
D. x 2 169 + y 2 5 = 1.