cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với đáy sa=a . gọi M,N lần lượt là trung điểm của SB và SD . Tính số đo góc giữa hai mặt phẳng (AMN) và (ABCD)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)
cho hình chóp SABCD có đáy là hình vuông tâm O cạnh a , SA = \(a\sqrt{2}\) SA vuông góc với đáy. Gọi M,N lần lượt là hình chiếu vuông góc của điểm A lên SB SD. Tính góc SA với (AMN)
Kẻ AE vuông góc SC (E thuộc SC)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\Rightarrow SC\perp\left(AMN\right)\)
Mà \(AE\perp SC\Rightarrow E\in\left(AMN\right)\)
\(\Rightarrow AE\) là hình chiếu vuông góc của SA lên (AMN)
\(\Rightarrow\widehat{SAE}\) là góc giữa SA và (AMN)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Delta SAC\) vuông cân tại A \(\Rightarrow AE=SE=\dfrac{1}{2}SC=a\)
\(\Rightarrow\Delta SAE\) vuông cân tại E \(\Rightarrow\widehat{SAE}=45^0\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = a 2 . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng
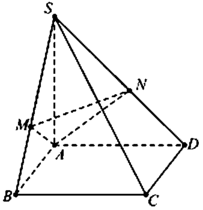
A. 45 °
B. 60 °
C. 90 °
Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Cho hình chóp SABCD đáy là hình vuông cạnh a , SA vuông góc đáy , góc giữa SB và đáy là 60°
a . cm các mặt bên của hình chóp là tam giác vuông . tính diện tích xung quanh của hình chóp
b. gọi H , K là hình chiếu của A lên SB , SD , cm AH vuông (SBC) , AK vuông (SCD)
c. cm HK vuông (SAC)
d. xác định và tính góc giữa SC và (ABCD) , SB và (SAC)
e. xđ và tính góc giữa 2 mặt ( SBD) và (ABCD)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
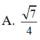
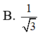
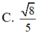
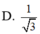
Chọn đáp án A
+ Ta có
![]()
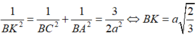
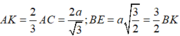
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
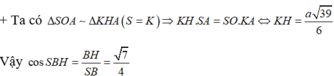
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai cạnh SB và SD sao cho SI/SB = SK/SD . Chứng minh:
a) BD ⊥ SC
b) IK ⊥mp(SAC)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với A B = a 2 ; B C = a và S A = S B = S C = S D = 2 a . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
A. 7 4
B. 1 3
D. 8 5
D. 2 3
Cho hình chóp SABCD đáy là hình vuông cạnh a. SA vuông góc với đáy, SA=2a. Gọi H,K,E lần lượt là hình chiếu của A lên SB,SC,SD. Tính VSAHKE
\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)