Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng 4 điểm D,M,I,N cùng thuộc 1 đường tròn

Những câu hỏi liên quan
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng:4 điểm D,M,I,N cùng thuộc 1 đường tròn
Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc một đường tròn
Đúng 1
Bình luận (1)
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng:
a. 4 điểm E,M,N,F cùng thuộc 1 đường tròn
b. 4 điểm D,M,I,N cùng thuộc 1 đường tròn
a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}\left(=90^0\right)\)
Do đó: ENMF là tứ giác nội tiếp
b: Xét tứ giác DNIM có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DNIM là tứ giác nội tiếp
Đúng 0
Bình luận (0)
a, Xét ΔENF vuông tại N
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
Xét ΔEMF vuông tại M
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
⇒ M,N,E,F cùng thuộc 1 đường tròn đường kính EF
b,Tương tự
Đúng 0
Bình luận (0)
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng:
a. 4 điểm E,M,N,F cùng thuộc 1 đường tròn
b. 4 điểm D,M,I,N cùng thuộc 1 đường tròn
a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}=90^0\)
Do đó: ENMF là tứ giác nội tiếp
hay E,N,M,F cùng thuộc 1 đường tròn
b: Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc 1 đường tròn
Đúng 1
Bình luận (1)
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng:4 điểm D,M,I,N cùng thuộc 1 đường tròn (giải bằng cách không sử dụng đến tứ giác nội tiếp)
Ta có: ΔDNI vuông tại N
nên ΔDNI nội tiếp đường tròn đường kính DI(1)
Ta có: ΔDMI vuông tại M
nên ΔDMI nội tiếp đường tròn đường kính DI(2)
Từ (1) và (2) suy ra D,M,I,N cùng thuộc 1 đường tròn
Đúng 1
Bình luận (0)
Cho tam giác DEF nhọn , vẽ 2 đường cao DM và EN cắt nhau tại I.
a. Chứng minh 4 điểm F , N , I , M thuộc 1 đường tròn.
b, Chứng minh 4 điểm D , N , M , E thuộc 1 đường tròn
a: Xét tứ giác FNIM có
\(\widehat{FNI}+\widehat{FMI}=180^0\)
nên FNIM là tứ giác nội tiếp
hay F,N,I,M cùng thuộc 1 đường tròn
b: Xét tứ giác DNME có
\(\widehat{DNE}=\widehat{DME}\left(=90^0\right)\)
nên DNME là tứ giác nội tiếp
hay D,N,M,E cùng thuộc 1 đường tròn
Đúng 1
Bình luận (1)
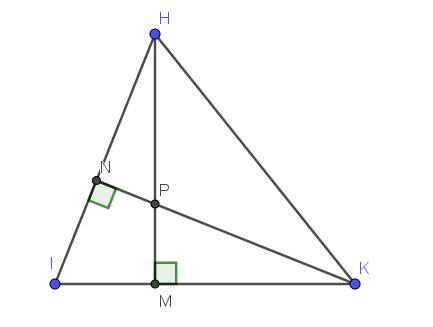
Cho tam giác HIK nhọn, kẻ hai đường cao HM và KN cắt nhau tại P. Chứng minh rằng:
1) 4 điểm H, N, M, K cùng thuộc 1 đường tròn.
2) 4 điểm I, N, P, M cùng cùng thuộc 1 đường tròn.
Lời giải:
1.
Xét tứ giác $HNMK$ có $\widehat{HNK}=\widehat{HMK}=90^0$. Mà 2 góc này cùng nhìn cạnh $HK$ nên $HNMK$ là tứ giác nội tiếp.
$\Rightarrow H,N,M,K$ cùng thuộc 1 đường tròn.
2.
Xét tứ giác $INPM$ có tổng 2 góc đối nhau $\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0$ nên $INPM$ là tứ giác nội tiếp.
$\Rightarrow I,N, P,M$ cùng thuộc 1 đường tròn.
Đúng 0
Bình luận (0)
Cho tam giác HIK nhọn, kẻ hai đường cao HM và KN cắt nhau tại P. Chứng minh rằng:
1) 4 điểm H, N, M, K cùng thuộc 1 đường tròn.
2) 4 điểm I, N, P, M cùng cùng thuộc 1 đường tròn.
1: Xét tứ giác HNMK có
\(\widehat{HNK}=\widehat{HMK}=90^0\)
=>HNMK là tứ giác nội tiếp đường tròn đường kính HK
=>H,N,M,K cùng thuộc 1 đường tròn
2: Xét tứ giác INPM có
\(\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0\)
=>INPM là tứ giác nội tiếp
=>I,N,P,M cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho tam giác DEF có đường cao DK, vẽ đường tròn đường kính EK và FK cắt DE, DF lần lượt tại M và N. Chứng minh 4 điểm D, M, K, N thuộc 1 đường thẳng
Xét \(\left(\dfrac{EK}{2}\right)\) có
ΔKME nội tiếp đường tròn
KE là đường kính
Do đó: ΔKME vuông tại M
Xét \(\left(\dfrac{FK}{2}\right)\) có
ΔFNK nội tiếp đường tròn
FK là đường kính
Do đó: ΔFNK vuông tại N
Xét tứ giác DMKN có \(\widehat{DMK}=\widehat{DNK}=\widehat{MDN}=90^0\)
nên DMKN là hình chữ nhật
hay D,M,K,N cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$. Các đường cao $AD$, $BE$, $CF$ cắt nhau tại $H$ và cắt đường tròn $(O)$ lần lượt tại $M$, $N$, $P$. Chứng minh rằng:
a) Tứ giác $AEHF$ nội tiếp.
b) Bốn điểm $B$, $C$, $E$, $F$ cùng thuộc một đường tròn.
c) $AE.AC AH.AD$ và $AD.BC BE.AC$.
d) $H$ và $M$ đối xứng nhau qua $BC$.
e) Xác định tâm đường tròn nội tiếp tam giác $DEF$.
Đọc tiếp
Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$. Các đường cao $AD$, $BE$, $CF$ cắt nhau tại $H$ và cắt đường tròn $(O)$ lần lượt tại $M$, $N$, $P$. Chứng minh rằng:
a) Tứ giác $AEHF$ nội tiếp.
b) Bốn điểm $B$, $C$, $E$, $F$ cùng thuộc một đường tròn.
c) $AE.AC = AH.AD$ và $AD.BC = BE.AC$.
d) $H$ và $M$ đối xứng nhau qua $BC$.
e) Xác định tâm đường tròn nội tiếp tam giác $DEF$.