Giải hàm số lượng giác sau:
\(\dfrac{sin2x-2sinx}{sin2x+2sinx}\)
Giải phương trình:
a, sin2x+2sinx-cosx+1=0
b, \(\dfrac{1}{cosx}+\dfrac{\sqrt{3}}{sinx}=2sin\)(x+\(\dfrac{\text{π}}{3}\))
b:
ĐKXĐ: \(\left\{{}\begin{matrix}cosx< >0\\sinx< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< >\dfrac{\Omega}{2}+k\Omega\\x\ne k\Omega\end{matrix}\right.\)
=>\(x\ne\dfrac{\Omega}{2}+\dfrac{k\Omega}{2}\)
\(\dfrac{1}{cosx}+\dfrac{\sqrt{3}}{sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left[sinx\cdot\cos\dfrac{\Omega}{3}+sin\left(\dfrac{\Omega}{3}\right)\cdot cosx\right]\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left(\dfrac{1}{2}\cdot sinx+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\)
=>\(\left(sinx+\sqrt{3}\cdot cosx\right)\left(\dfrac{1}{cosx\cdot sinx}-1\right)=0\)
=>\(2\cdot\left(sinx\cdot\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\cdot\left(\dfrac{2}{2\cdot sinx\cdot cosx}-1\right)=0\)
=>\(2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\cdot\left(\dfrac{2}{sin2x}-1\right)=0\)
=>\(\left[{}\begin{matrix}sin\left(x+\dfrac{\Omega}{3}\right)=0\\\dfrac{2}{sin2x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=k\Omega\\sin2x=2\left(loại\right)\end{matrix}\right.\)
=>\(x=-\dfrac{\Omega}{3}+k\Omega\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 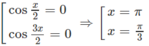
Ta có: f(0) = 0,
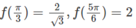
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Giải phương trình: 1+2sin^2x - 3√2sinx+sin2x \2sinx cosx =1
Tìm giá trị lớn nhất và nhỏ nhất của hàm số: f(x)=2sinx+sin2x trên nửa khoảng 0 ; 3 2 π
Giải phương trình sin 2 x + 2 sin x - π 4 = 1
![]()
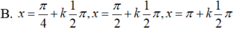
![]()
![]()
Giải phương trình sin2x + 2sinx – 3=0
![]()
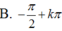
![]()
![]()
Chứng minh
a) \(\frac{1-sin2x}{1+sin2x}=cot^2\left(\frac{\pi}{4}-x\right)\)
b) \(\frac{Sin2x-2sinx}{sin2x+2sinx}=-tan^2\frac{x}{2}\)
\(\frac{1-sin2x}{1+sin2x}=\frac{sin^2x+cos^2x-2sinx.cosx}{sin^2x+cos^2x+2sinx.cosx}=\frac{\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}\)
\(=\frac{\left[\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\right]^2}{\left[\sqrt{2}.sin\left(x+\frac{\pi}{4}\right)\right]^2}=tan^2\left(\frac{\pi}{4}-x\right)\)
Bạn coi lại đề, vế phải là tan chứ ko phải cot
\(\frac{sin2x-2sinx}{sin2x+2sinx}=\frac{2sinx.cosx-2sinx}{2sinx.cosx+2sinx}=\frac{2sinx\left(cosx-1\right)}{2sinx\left(cosx+1\right)}\)
\(=\frac{cosx-1}{cos+1}=\frac{1-2sin^2\frac{x}{2}-1}{2cos^2\frac{x}{2}-1+2}=\frac{-2sin^2\frac{x}{2}}{2cos^2\frac{x}{2}}=-tan^2\frac{x}{2}\)
giải phương trình:
(2cosx-1)(2sinx+cosx)=sin2x-sinx
Lời giải:
PT $\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=2\sin x\cos x-\sin x$
$\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=\sin x(2\cos x-1)$
$\Leftrightarrow (2\cos x-1)(\sin x+\cos x)=0$
$\Rightarrow 2\cos x=1$ hoặc $\sin x=-\cos x=\cos (\pi -x)=\sin (x-\frac{\pi}{2})$
Đến đây thì đơn giản rồi.
giải pt 2sinx + cos3x +sin2x=1+sin4x
\(\Leftrightarrow2sinx+cos3x+sin2x-sin4x-1=0\)
\(\Leftrightarrow2sinx-1+cos3x-2cos3x.sinx=0\)
\(\Leftrightarrow2sinx-1-cos3x\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(1-cos3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cos3x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)