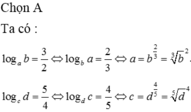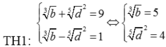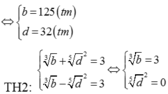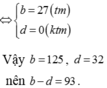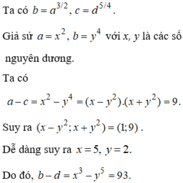Cho a,b,c là các số dương thỏa mãn a+b+c<=1. Chứng minh 1/(a+1) + 1(b+1) +1/(c+1)>= (9/4)

Những câu hỏi liên quan
1.cho a, b,c là các số thực dương thỏa mãn a^3 /(a^2+b^2) + b^3/(b^2+c^2) + c^3/(c^2+a^2) >= (a+b+c)/2
2.cho a, b,c là các số thực dương thỏa mãn (a^3 +b^3+c^3)/2abc + (a^2+ b^2)/c^2 + (b^2+c^2)/(a^2+bc) + (c^2+a^2)/b^2+ac) >= 9/2
Cho a, b, c là các số dương thỏa mãn a + b + c = 8
CMR: \(\dfrac{a+b}{abc}\ge\dfrac{1}{4}\)
BDT <=> \(4\left(a+b\right)\ge abc\)
<=> \(4\left(a+b\right)\ge ab\left(8-a-b\right)\)
<=> \(4\left(a+b\right)\ge8ab-ab\left(a+b\right)\)
<=> \(\left(a+b\right)\left(ab+4\right)\ge8ab\)
Áp dụng Bdt Bunhiacopxki, ta có:
\(\left(a+b\right)\left(ab+4\right)\ge\left(a\sqrt{b}+2\sqrt{b}\right)^2=b\left(a+2\right)^2\)
Cần chứng minh \(b\left(a+2\right)^2\ge8ab\)
<=> \(a^2+4a+4\ge8a\)
<=> \(a^2-4a+4\ge0\)
<=> \(\left(a-2\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra <=> a = b = 2; c = 4
Đúng 2
Bình luận (0)
Cho a,b,c,d là các số nguyên dương,
a
≠
1
;
c
≠
1
thỏa mãn
log
a
b
3
2
,
log
c
d
5
4
và
a
-
c
9
. Khi đó
b
-
d
A.93 B.9 C.13 D.21
Đọc tiếp
Cho a,b,c,d là các số nguyên dương,
a ≠ 1 ; c ≠ 1 thỏa mãn log a b = 3 2 ,
log c d = 5 4 và a - c = 9 . Khi đó b - d
A.93
B.9
C.13
D.21
Cho a, b, c, d là các số nguyên dương,
a
≠
1
;
c
≠
1
thỏa mãn
log
a
b
3
2
;
log
c
d
5
4
và
a
−
c
9
. Khi đó b – d bằng A. 93 B. 9 C. 13 D. 21
Đọc tiếp
Cho a, b, c, d là các số nguyên dương, a ≠ 1 ; c ≠ 1 thỏa mãn log a b = 3 2 ; log c d = 5 4 và a − c = 9 . Khi đó b – d bằng
A. 93
B. 9
C. 13
D. 21
Cho a, b, c, d là các số nguyên dương thỏa mãn
log
a
b
3
2
,
log
c
d
5
4
. Nếu a-c9, thì b-d nhận giá trị nào? A. 85. B. 71. C. 76. D. 93.
Đọc tiếp
Cho a, b, c, d là các số nguyên dương thỏa mãn log a b = 3 2 , log c d = 5 4 . Nếu a-c=9, thì b-d nhận giá trị nào?
A. 85.
B. 71.
C. 76.
D. 93.
Cho a, b, c, d là các số nguyên dương thỏa mãn
log
a
b
3
2
,
log
c
d
5
4
. Nếu
a
−
c
9
, thì
b
−
d
nhận giá trị nào? A. 85 B. 71 C. 76 D. 93.
Đọc tiếp
Cho a, b, c, d là các số nguyên dương thỏa mãn log a b = 3 2 , log c d = 5 4 . Nếu a − c = 9 , thì b − d nhận giá trị nào?
A. 85
B. 71
C. 76
D. 93.
cho a,b,c là các số không dương thỏa mãn a^2+b^2+c^2=(a-b)^2+(b-c)^2+(c-a)^2 và ab+bc+ca=9 tính a+b+c
Cho các số dương a, b, c thỏa mãn: a+b+c=1. CMR: \(4.\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\le\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+9\)
Cho a;b;c là ba số thực dương,
a
1
và thỏa mãn
log
2
a
b
c
+
log
a
b
3
c
3
+
b
c...
Đọc tiếp
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Đúng 0
Bình luận (0)