giải phương trình (đoán nghiệm)
x5-5x4-2x3+17x2-13x+2=0
Những câu hỏi liên quan
Cho hai đa thức:
P
x
x
5
-
3
x
2
+
7
x
4
-
9
x
3
+
x
2
-
1
4
x
Q
x
5
x
4
-...
Đọc tiếp
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1
3
x
-
y
2
3
x
-
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1 3 x - y = 2 3 x - 3 y = 2
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a
)
4
x
−
4
y
2
−
2
x...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) 4 x − 4 y = 2 − 2 x + 2 y = − 1 b ) 1 3 x − y = 2 3 x − 3 y = 2
a)
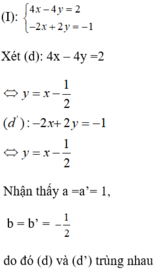
Vậy hệ phương trình có vô số nghiệm.
b)
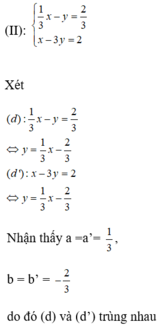
Vậy hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I):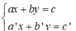 
Gọi (d): ax + b = c và (d’): a’x + b’ = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’
Đúng 0
Bình luận (0)
giải phương trình (đoán nghiệm)
a) x5-5x4-2x3+17x2-13x+2=0
b) x5-x3-x2+1=0
Cho phương trình:
2
x
3
+
x
2
-
3
x
+
1
2
3
x
-
1
3
x
-
1
Tính tổng các nghiệm cùa phương trình là : A.1 B.2 C.3 D.4
Đọc tiếp
Cho phương trình: 2 x 3 + x 2 - 3 x + 1 = 2 3 x - 1 3 x - 1
Tính tổng các nghiệm cùa phương trình là :
A.1
B.2
C.3
D.4
Điều kiện. x≥1/3
Ta có:
2 x 3 + x 2 - 3 x + 1 = 2 ( 3 x - 1 ) 3 x - 1 ⇔ 2 x 3 + x 2 + 1 = 2 ( 3 x - 1 ) 3 + ( 3 x - 1 ) 2 + 1 f ( x ) = f ( 3 x - 1 )
Xét hàm số f(t) = 2t3+ t2+ 1 liên tục tên R.
Ta có: đạo hàm f’ (t) = 6t2+2t> 0 với t>0 .
Do đó ; hàm số f(t) đồng biến trên (0; +∞).
f ( x ) = f ( 3 x - 1 ) ⇔ x = 3 x - 1 ⇔ x 2 = 3 x - 1 ⇔ x = 3 - 5 2 > 1 3 x = 3 + 5 2 > 1 3
Tổng các nghiệm là 3.
Chọn C.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
5
-
2
x
3
+
x
+
1
x
-
1
3
x
-
1...
Đọc tiếp
Giải các phương trình sau: 5 - 2 x 3 + x + 1 x - 1 3 x - 1 = x + 2 1 - 3 x 9 x - 3
5 - 2 x 3 + x + 1 x - 1 3 x - 1 = x + 2 1 - 3 x 9 x - 3 Đ K X Đ : x ≠ 1 3 ⇔ 5 - 2 x 3 x - 1 3 3 x - 1 + 3 x + 1 x - 1 3 3 x - 1 = x + 2 1 - 3 x 3 3 x - 1
⇔ (5 – 2x)(3x – 1) + 3(x + 1)(x – 1) = (x + 2)(1 – 3x)
⇔ 15x – 5 – 6 x 2 + 2x + 3 x 2 – 3 = x – 3 x 2 + 2 – 6x
⇔ - 6 x 2 + 3 x 2 + 3 x 2 + 15x + 2x – x + 6x = 2 + 5 + 3
⇔ 22x = 10 ⇔ x = 5/11 (thỏa mãn)
Vậy phương trình có nghiệm x = 5/11
Đúng 0
Bình luận (0)
Cho hai phương trình
x
2
−
13
x
+
2
m
0
(
1
)
v
à
x
2
−
4
x
+
m
0
(
2
)
. Xác định m để một nghiệm phương trình (1) gấp đôi một nghiệm phương trình (2) A. −45 B. −5 C. 0 và −5 D. Đáp án khác
Đọc tiếp
Cho hai phương trình x 2 − 13 x + 2 m = 0 ( 1 ) v à x 2 − 4 x + m = 0 ( 2 ) . Xác định m để một nghiệm phương trình (1) gấp đôi một nghiệm phương trình (2)
A. −45
B. −5
C. 0 và −5
D. Đáp án khác
Gọi nghiệm của phương trình (2) là x0 (x0 ≠ 0)
thì nghiệm phương trình (1) là 2x0
Thay x0; 2x0 lần lượt vào phương trình (2) và (1)
ta được
2 x 0 2 − 13.2 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0
⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0 ⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 4 x 0 2 − 16 x 0 + 4 m = 0
⇔ 10x0 = −2m ⇔ x 0 = − m 5
Do x0 ≠ 0 nên m ≠ 0
Thay x 0 = − m 5 vào phương trình (2)
ta được − m 5 2 − 4. − m 5 + m = 0
⇔ m 2 25 + 4 m 5 + m = 0
⇔ m 2 25 + 9 m 5 = 0 ⇒ m = 0 m = − 45
Kết hợp m ≠ 0 ta được m = −45
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Bài 1: Tính giá trị của biểu thức.
a. A = x3-30x2-31x + 1 tại x = 31
b. B = x5-15x4+ 16x3-29x2+ 13x tại x = 14
c. C = x4 - 17x3 + 17x2 - 17x + 20 tại x = 16
d. D = x10 - 13x9 + 13x8 - 13x7 +...+ 13x2 - 13x + 10 tại x = 12
a: Ta có: x=31
nên x-1=30
Ta có: \(A=x^3-30x^2-31x+1\)
\(=x^3-x^2\left(x-1\right)-x^2+1\)
\(=x^3-x^3+x^2-x^2+1\)
=1
c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(=20-x=4\)
Đúng 1
Bình luận (0)
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=10-x\)
=-2
Đúng 1
Bình luận (0)
Bài 1: Tính giá trị của biểu thức.
a. A = x3-30x2-31x + 1 tại x = 31
b. B = x5-15x4+ 16x3-29x2+ 13x tại x = 14
c. C = x4 - 17x3 + 17x2 - 17x + 20 tại x = 16
d. D = x10 - 13x9 + 13x8 - 13x7 +...+ 13x2 - 13x + 10 tại x = 12
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+1+9\)
\(=-x+10=-2\)
Đúng 1
Bình luận (0)
Số nghiệm phương trình:
1
−
5
x
4
+
5
x
2
+
10
1
+
5
0
là: A. 0 B. 4 C. 1 D. 2
Đọc tiếp
Số nghiệm phương trình: 1 − 5 x 4 + 5 x 2 + 10 1 + 5 = 0 là:
A. 0
B. 4
C. 1
D. 2
Đặt t = x 2 , t ≥ 0 , phương trình trở thành:
1 − 5 t 2 + 5 t + 10 1 + 5 = 0 *
Phương trình (*) có hệ số a . c = 1 − 5 10 1 + 5 = − 40 < 0 ⇒ phương trình có hai nghiệm trái dấu
Vậy phương trình đã cho có 2 nghiệm phân biệt
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)