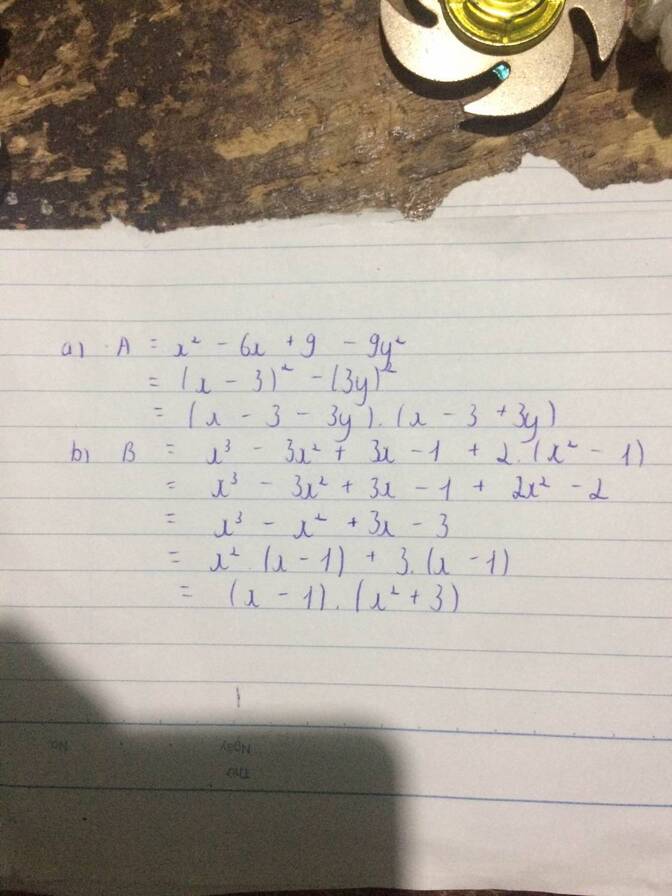Ta có:  x 2 + 6 x + 9 = x 2 + 2 . x . 3 + 3 2 = ( x + 3 ) 2 .

Ta có:  x 2 + 6 x + 9 = x 2 + 2 . x . 3 + 3 2 = ( x + 3 ) 2 .

a ) x=0; x = -(căn bậc hai(7)*i-3)/8;x = (căn bậc hai(7)*i+3)/8;

b ) -(y-x-3)*(y+x+3)

a) \(12x^3-9x^2+3x\)

\(=3x\left(4x^2-3x+1\right)\)

b) \(x^2-y^2+6x+9\)

\(=\left(x^2+6x+9\right)-y^2\)

\(=\left(x+3\right)^2-y^2\)

\(=\left(x+y+3\right)\left(x-y+3\right)\)

a) (x + 2)(x + 4).              b) 2(x + 6)(x + l).

c) 3(3x + 5)(x + l).           d) (6x -7y)(x + y).

Chọn B

a) $4x^2+4x+1$

$=(2x)^2+2\cdot2x\cdot1+1^2$

$=(2x+1)^2$

b) $x^2+6x-y^2+9$

$=(x^2+6x+9)-y^2$

$=(x^2+2\cdot x\cdot3+3^2)-y^2$

$=(x+3)^2-y^2$

$=(x+3-y)(x+3+y)$

$\text{#}Toru$

a: \(4x^2+4x+1\)

\(=\left(2x\right)^2+2\cdot2x\cdot1+1^2\)

\(=\left(2x+1\right)^2\)

b: \(x^2+6x-y^2+9\)

\(=\left(x^2+6x+9\right)-y^2\)

\(=\left(x+3\right)^2-y^2\)

\(=\left(x+3+y\right)\left(x+3-y\right)\)

a) \(A=x^2-6x+9-9y^2\)

\(=\left(x-3\right)^2-\left(3y\right)^2\)

\(=\left(x-3-3y\right)\left(x-3+3y\right)\)

b) \(B=x^3-3x^2+3x-1+2\left(x^2-1\right)\)

\(=\left(x-1\right)^3+\left(2x+2\right)\left(x-1\right)\)

\(=\left(x-1\right)\left[\left(x-1\right)^2+2x+2\right]\)

\(=\left(x-1\right).\left(x^2+3\right)\)

a, \(A=\left(x-3\right)^2-9y^2=\left(x-3-3y\right)\left(x-3+3y\right)\)

b, \(B=\left(x-1\right)^3+2\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left[\left(x-1\right)^2+2\left(x+1\right)\right]\)

\(=\left(x-1\right)\left(x^2-2x+1+2x+2\right)=\left(x-1\right)\left(x^2+3\right)\)

a) Áp dụng HĐT 1 thu được ( 2 x   +   y ) 2 .

b) Áp dụng HĐT 3 với A = 2x + l; B = x - l thu được

[(2x +1) + (x -1)] [(2x +1) - (x -1)] rút gọn thành 3x(x + 2).

c) Ta có: 9 - 6x +  x 2  -  y 2 = ( 3   -   x ) 2  -  y 2  = (3 - x - y)(3 -x + y).

d) Ta có: -(x + 2) + 3( x 2  - 4) = -{x + 2) + 3(x + 2)(x - 2)

= (x + 2) [-1 + 3(x - 2)] = (x + 2)(3x - 7).

c) \(5x^2+3y+15x+xy=5x\left(x+3\right)+y\left(x+3\right)=\left(x+3\right)\left(5x+y\right)\)

d) \(x^2+6x+9-y^2=\left(x+3\right)^2-y^2=\left(x+3-y\right)\left(x+3+y\right)\)

e) \(x^2-y^2+2x+1=\left(x^2+2x+1\right)-y^2=\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)

f) \(x^2-2xy-9+y^2=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-3^2=\left(x-y-3\right)\left(x-y+3\right)\)

c: \(5x^2+15x+3y+xy\)

\(=5x\left(x+3\right)+y\left(x+3\right)\)

\(=\left(x+3\right)\left(5x+y\right)\)

d: \(x^2+6x+9-y^2\)

\(=\left(x+3\right)^2-y^2\)

\(=\left(x+3-y\right)\left(x+3+y\right)\)

e: \(x^2+2x+1-y^2\)

\(=\left(x+1\right)^2-y^2\)

\(=\left(x+1-y\right)\left(x+1+y\right)\)

f: \(x^2-2xy+y^2-9\)

\(=\left(x-y\right)^2-9\)

\(=\left(x-y-3\right)\left(x-y+3\right)\)