Tìm giá trị của biến số
A=(x+1).(y^2 -6) có giá trị bằng 0
tìm các giá trị của biến để biểu thức (x+1) ^2(y^2-6) có giá trị bằng 0
(x+1)2(y2-6)=0
=> \(\orbr{\begin{cases}\left(x+1\right)^2=0\\y^2-6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x+1=0\\y^2=6\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-1\\y=\pm\sqrt{6}\end{cases}}}\)
vậy........
tìm giá trị của biến số để mỗi biểu thức sau có giá trị bằng 0:
a) (x+1) (x^2 +1)
b) 5y^2 -20
c) |x-2|-1
d) |y-2|+5
giúp e với ạ huhu
a) \(\left(x+1\right)\left(x^2+1\right)=0\)
Vì \(\left(x^2+1\right)>0\forall x\)
\(\Rightarrow x=-1\)
b) \(5y^2-20=0\)
\(y^2-4=0\)
\(\left(y-2\right)\left(y+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\)
a, Ta có : \(\left(x+1\right)\left(x^2+1>0\right)=0\Leftrightarrow x=-1\)
b, \(5y^2=20\Leftrightarrow y^2=4\Leftrightarrow\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\)
c, \(\left|x-2\right|-1=0\Leftrightarrow\left|x-2\right|=1\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
d, \(\left|y-2\right|+5=0\)( vô lí )
Vậy ko có gtr y để bth bằng 0
c) \(\left|x-2\right|-1=0\)
\(\left|x-2\right|=1\)
\(\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
d) \(\left|y-2\right|+5=0\)
\(\left|y-2\right|=-5\)
Vì \(\left|y-2\right|\ge0\forall y\)
⇒ pt vô nghiệm
Tìm giá trị của biến số để mỗi biểu thức sau có giá trị bằng 0:
a) \(5y^2-20\)
b) \(\left|y-1\right|+5\)
Tìm giá trị của biến số để biểu thức(x+1)(x^2+1)có giá trị bằng 0
\(\left(x+1\right)\left(x^2+1\right)=0\)
=> \(\left(x+1\right)=0\) hoac \(\left(x^2+1\right)=0\)
\(x+1=0\Rightarrow x=-1\)
\(x^2+1=0\Rightarrow x^2=-1\Rightarrow x=-1\)
hok tot
(x+1)(x2+1)=0
Ta có: x2+1 >0 với mọi x
=> Để (x+1)(x2+1)=0
=> x+1=0
=> x=-1
\(\left(x+1\right)\left(x^2+1\right)=0\)
Để biểu thức trên = 0 => \(\orbr{\begin{cases}x+1=0\\x^2+1=0\end{cases}}\)
\(x+1=0\Rightarrow x=-1\)
\(x^2+1=0\Rightarrow x^2=-1\Rightarrow x=-1\)
Vậy x = -1 thì biểu thức \(\left(x+1\right)\left(x^2+1\right)\)có giá trị bằng 0
tìm giá trị của biến để biểu thức sau đây có giá trị bằng 0
A=(x-2)2+(y+3)2
\(\left(x-2\right)^2+\left(y+3\right)^2\ge0\forall x;y\)
Dấu = xảy ra khi \(\hept{\begin{cases}\left(x-2\right)^2=0\\\left(y+3\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y=-3\end{cases}}}\)
Vậy để biểu thức cs giá trị = 0 thì x=2, y=-3
\(2x^2-3x=0\)
\(x\left(2x-3\right)=0\)
\(\hept{\begin{cases}x=0\\2x-3=0\end{cases}\Rightarrow\hept{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}}\)
tìm giá trị của các biến để các biểu thức sau đây có giá trị = 0
a) 16 - x 2
b) (x + 1)2 + ( 2 y - 3 )10
a.\(16-x^2=0\)
\(\Leftrightarrow x^2=16\)
\(\Leftrightarrow x^2=4^2\)
\(\Leftrightarrow x=\pm4\)
b.\(\left(x+1\right)^2+\left(2y-3\right)^{10}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\\left(2y-3\right)^{10}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2y-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\)
Hãy vẽ đồ thị của các hàm số y = 2 x 2 , y = - 2 x 2 . Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số y = a x 2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số y = a x 2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Vẽ hình:
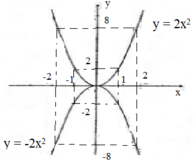
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Tìm giá trị của biến số để giá trị của biểu thức sau bằng 0
(x-1)(x+1)(x^2+1/2)
\(\left(x-1\right)\left(x+1\right)\left(x^2+\frac{1}{2}\right)=0\)
Vì \(x^2+\frac{1}{2}>0\) nên \(\Rightarrow\)\(\orbr{\begin{cases}x-1=0\\x+1=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Vậy....
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
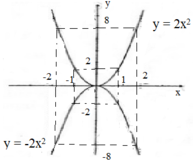
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
1. Cho biểu thức A= \(\sqrt{4-2x}\)
a) Tìm điều kiện của x để biểu thức có nghĩa.
b) Tìm giá trị của biểu thức khi x=2, x=0,x=1,x=-6,x=-10.
c) Tìm giá trị của biến x để giá trị của biểu thức bằng 0? Bằng 5? Bằng 10?
2. Cho biểu thức P= \(\frac{9}{2\sqrt{x}-3}\)
a) Tìm điều kiện của X để biểu thức P xác định..
b) Tính giá trị của biểu thức khi x=4, x=100
c) Tìm giá trị của x để P=1, P=7
d) Tìm các số nguyên x để giá trị của P cũng là một số nguyên.
3. Cho biểu thức \(\frac{2\sqrt{x}+9}{\sqrt{x}+1}\)
a) Tìm điều kiện xác định của x để biểu thức Q được xác định.
b) Tính giá trị của biểu thức khi x=0,x=1,x=16.
c) Tìm giá trị của x để Q=1,Q=10.
d) Tìm các số nguyên x để giá trị của Q cũng là một số nguyên.
Giải hộ với ạ! Gấp lắm T.T
1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)
2) a) P xác định \(\Leftrightarrow x\ge0\)và \(2\sqrt{x}-3\ne0\Leftrightarrow\sqrt{x}\ne\frac{3}{2}\Leftrightarrow x\ne\frac{9}{4}\)
b) Thay x = 4 vào P, ta được: \(P=\frac{9}{2\sqrt{4}-3}=\frac{9}{1}=9\)
Thay x = 100 vào P, ta được: \(P=\frac{9}{2\sqrt{100}-3}=\frac{9}{17}\)
c) P = 1 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=1\Leftrightarrow2\sqrt{x}-3=9\Leftrightarrow\sqrt{x}=6\Leftrightarrow x=36\)
P = 7 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=7\Leftrightarrow2\sqrt{x}-3=\frac{9}{7}\)
\(\Leftrightarrow2\sqrt{x}=\frac{30}{7}\Leftrightarrow\sqrt{x}=\frac{15}{7}\Leftrightarrow x=\frac{225}{49}\)
d) P nguyên \(\Leftrightarrow9⋮2\sqrt{x}-3\)
\(\Leftrightarrow2\sqrt{x}-3\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Lập bảng:
| \(2\sqrt{x}-3\) | \(1\) | \(-1\) | \(3\) | \(-3\) | \(9\) | \(-9\) |
| \(\sqrt{x}\) | \(2\) | \(1\) | \(3\) | \(0\) | \(6\) | \(-3\) |
| \(x\) | \(4\) | \(1\) | \(9\) | \(0\) | \(36\) | \(L\) |
Vậy \(x\in\left\{1;4;9;0;36\right\}\)