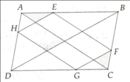
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng cắt BD, AB, AD ở E ,G, F chứng minh DE^2=FE/EG*BE^2

Những câu hỏi liên quan
1.Cho hình bình hành ABCD một đường thẳng cắt AB, AD, AC lần lượt tại E, F, G .Chứng minh : AB/AE+AD/AF=AC/AG
2.Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng cắt BD, AB, AD ở E, G, F chứng minh DE^2=FE/EG*BE^2
Qua đỉnh C của hình bình hành ABCD, kẻ đường thẳng cắt BD, AB, AD ở E,G,F. Chứng minh:
a. \(DE^2=\dfrac{FE}{EG}.BE^2\)
b. \(CE^2=FE.GE\)
Làm câu b trước rồi giải a sau đc k nhỉ?
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD cắt AB ở E, cắt AD ở F
a.Tứ giác BECD là hình gì?Vì sao?
b.Chứng minh 3 đừng thẳng AC, BF, DE đồng quy
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD cắt AB ở E, cắt AD ở F
a.Tứ giác BECD là hình gì Vì sao
b.Chứng minh 3 đừng thẳng AC, BF, DE đồng quy
Đúng 0
Bình luận (0)
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD cắt AB ở E, cắt AD ở F
a.Tứ giác BECD là hình gì Vì sao
b.Chứng minh 3 đừng thẳng AC, BF, DE đồng quy
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ qua F song song với BD cắt CD ở G. Chứng minh A H . C D = A D . C G .
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD, cắt AB ở E, cắt AD ở F.
a) Tứ giác BECD là hình gì? Vì sao?
b) Cmr ba đường thẳng AC,BF,DE đồng quy
cho hình bình hành ABCD, O là giao điểm hai đường chéo . Gọi M là điểm trên AC qua M kẻ đường thẳng //BC cắt AB tại E, kẻ đường thẳng //CD cắt AD tại G, EG cắt AC tại I. Chứng minh EG//BD
Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.

Áp dụng định lý Thalès, ta có:
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)
Bài 6. Qua đỉnh C của hbh ABCD kẻ đường thẳng song song với BD, cắt AB ở E, cắt AD ở F. a) Tứ giác BECD là hình gì ? Vì sao? b) Chứng minh AC, BF, DE đồng quy.
a/
Ta có
AB//CD (cạnh đối hbh) => BE//CD
CE//BD (gt)
=> BECD là hình bh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
b/
Ta có
BE=CD (cạnh đối hbh)
AB=CD (cạnh đối hbh)
=> BE=AB => BF là đường trung tuyến của tg AEF
Ta có
CF//BD (gt)
AD//BC (cạnh đối hbh) => DF//BC
=> BCFD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
BC=AD (cạnh đối hbh)
BC=DF (cạnh đối hbh)
=> AD=DF => DE là đường trung tuyến của tg AEF
Ta có
BD=CE (cạnh đối hbh)
BD=CF (cạnh đối hbh)
=> CE=CF => AC là trung tuyến của tg AEF
=> AC; BF; DE đồng quy (trong tg 3 đường trung tuyến đồng quy)
Đúng 1
Bình luận (0)
Bài 3: Qua đỉnh C của hình bình hành ABCD kẻ các đường thẳng song song với BD cắt AB ở E ,cắt AD ở F.
a) Tứ giác BECD là hình gì?
b) C/m: 3 đườngthẳng AC; BF; DE đồng qui
A) ta có:
AD//BC (ABCD là hình bình hành)
=>góc DAB= góc CBE(2 góc so le trong)
và góc ADB=góc DBC (2 góc so le trong)
mà góc DBC= góc BCE ( BD//CE)
nên góc ADB= góc BCE
Xét tam giác ABD và tam giác BEC
góc DAB= góc CBE(chứng minh trên)
góc ADB= góc BCE(chứng minh trên)
AD=BC(ABCD là hình bình hành)
suy ra: tam giác ABD = tam giác BEC(g-c-g)
suy ra: BD=CE(2 cạnh tương ứng)
mà BD//CE(giả thiết)
nên BECD là hình bình hành
Đúng 1
Bình luận (0)
a: Xét tứ giác BECD có
BE//CD
BD//CE
Do đó: BECD là hình bình hành
Đúng 0
Bình luận (0)