Cho tam giác ABC . Tìm điểm M sao cho →MA 2→MB 3→MC →0

Những câu hỏi liên quan
Cho tam giác ABC cố định . tìm điểm M hoặc tập hợp điểm M sao cho
véc tơ MA + 3 véc tơ MB - 2 véc tơ MC = véc tơ 0
3 véc tơ MA - véc tơ MB - 2 véc tơ MC = véc tơ 0
Cho tam giác ABC. Tìm điểm M thỏa mãn
M
A
→
+
M
B
→
+
2
M
C
→
0
→
A. M là trung điểm cạnh IC , với I là trung điểm của cạnh AB B.M trùng với đỉnh C của tam giác ABC...
Đọc tiếp
Cho tam giác ABC. Tìm điểm M thỏa mãn M A → + M B → + 2 M C → = 0 →
A. M là trung điểm cạnh IC , với I là trung điểm của cạnh AB
B.M trùng với đỉnh C của tam giác ABC
C.M là trọng tâm của tam giác ABC.
D. M là đỉnh của hình bình hành MCAB
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| 2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Đọc tiếp
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| =2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
Đúng 1
Bình luận (0)
Cho tam giác ABC. Tìm điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\) ?
Gọi D là trung điểm của cạnh AB, ta có:
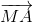 +
+ = 2
= 2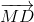
Đẳng thức đã cho trở thành:
2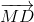 + 2
+ 2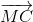 =
= 
=> 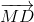 +
+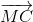 =
= 
Đẳng thức này chứng tỏ M là trung điểm của CD
Đúng 0
Bình luận (0)
cho tam giác ABC tìm tập hợp điểm M sao cho \(\overrightarrow{MB}^2+\overrightarrow{MC}^2-\overrightarrow{MA}^2=0\)
Cho tam giác ABC. Tìm quỹ tích những điểm M thỏa mãn: \(MA^2+\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MA}.\overrightarrow{MC}=0\)
\(\Leftrightarrow\overrightarrow{MA}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)=\overrightarrow{0}\)
=>vecto MA=0 hoặc M là trọng tâm của ΔABC
=>M là trọng tâm của ΔABC hoặc M trùng với A
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Trong tam giác đều ABC lấy điểm M sao cho MB = MC và góc BMC = 900.
a. Cm tam giác AMB = tam giác AMC.
b. Trong tam giác BMC lấy điểm E sao cho góc EBC = góc ECM = 300. Chứng minh tam giác MCE cân.
c. Giả sử điểm M nằm trong tam giá ABC sao cho MA : MB : MC = 3 : 4 : 5. Tính góc AMB.
Ai xong và đúng mình k cho
Em tham khảo nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
cho tam giác ABC : a)tìm các điểm M và N sao cho vector MA - vector MB + vector MC = vector 0 và 2 vector NA + vector NB + vector NC = vector 0
a: \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}=\overrightarrow{CM}\)
=>BAMC là hình bình hành
=>M là điểm thỏa mãn BAMC là hình bình hành
Gọi K là trung điểm của BC
\(2\overrightarrow{NA}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\overrightarrow{NA}+2\overrightarrow{NK}=\overrightarrow{0}\)
=>\(\overrightarrow{NA}+\overrightarrow{NK}=\overrightarrow{0}\)
=>N là trung điểm của AK
Đúng 0
Bình luận (0)
Cho tam giác ABC Xác định vị trí điểm M sao cho vecto MA - vecto MB + vecto MC = vecto 0
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
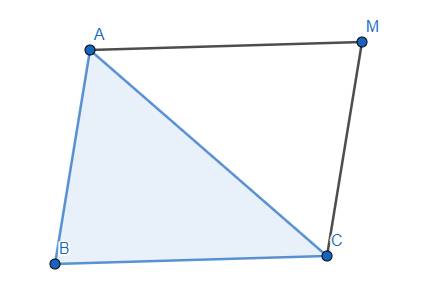
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
Đúng 1
Bình luận (0)