Các câu hỏi tương tự
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
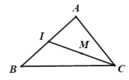
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
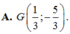
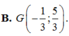
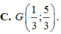
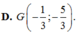
Cho tam giác ABC với trọng tâm G. Gọi A,B,C lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác ABC thành tam giác ABC là A. Phép vị tự tâm G, tỉ số k2 B. Phép vị tự tâm G, tỉ số k-2 C. Phép vị tự tâm G, tỉ số k-3 D. Phép vị tự tâm G, tỉ số k3
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác A'B'C' thành tam giác ABC là
A. Phép vị tự tâm G, tỉ số k=2
B. Phép vị tự tâm G, tỉ số k=-2
C. Phép vị tự tâm G, tỉ số k=-3
D. Phép vị tự tâm G, tỉ số k=3
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC? A. Phép vị tự tâm G, tỉ số 2 B. Phép vị tự tâm G, tỉ số –2 C. Phép vị tự tâm G, tỉ số
−
2
3
D. Phép vị tự tâm G, tỉ số
−
1
2
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC?
A. Phép vị tự tâm G, tỉ số 2
B. Phép vị tự tâm G, tỉ số –2
C. Phép vị tự tâm G, tỉ số − 2 3
D. Phép vị tự tâm G, tỉ số − 1 2
Cho hình chóp s.abcd đáy là hbh. Gọi H K lần lượt là trung điểm SA SC. G là trọng tâm tam giác ABC a)GHK và ABCD b) Tìm giao điểm M của SD và GHK c) Gọi E là trung điểm của HK.C/m G E M thẳng hàng
cho tam giác ABC nội tiếp đường tròn tâm I, có đỉnh A thuộc đường thẳng d:x+y-2=0, điểm D(-2;1) là chân đường cao của tam giác ABC hạ từ A. Gọi E(3;1) là chân đường vuông góc hạ từ B xuống AI, điểm P(2;1) thuộc cạnh AC. Tìm tọa độ các đỉnh của tam giác ABC
Cho
∆
A
B
C
có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM? A.
V
A
;
-
1
2
B.
V
G...
Đọc tiếp
Cho ∆ A B C có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM?
A. V A ; - 1 2
B. V G ; 1 2
C. V G ; - 2
D. V G ; - 1 2
Cho hình chóp s.abcd , có đáy ABCD là hbh. Gọi H, K lần lượt là trung điểm SA, SC. Gọi G là trọng tâm tam giác ABC.
a) GHK và ABCD
b) Tìm giao điểm M của SD và GHK
c) Gọi E là trung điểm của HK. C/m G, E, M thẳng hàng
Ai giải giúp em với ạ e cần gấp ạ.E cảm ơnCho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H và K lần lượt là trung điểm của SA và SC, G là trọng tâm của tam giác ABC. a) Tìm giao điểm M của SD và (GHK). b) Gọi E trung điểm của HK. Chứng minh G, E, M thẳng hàng.