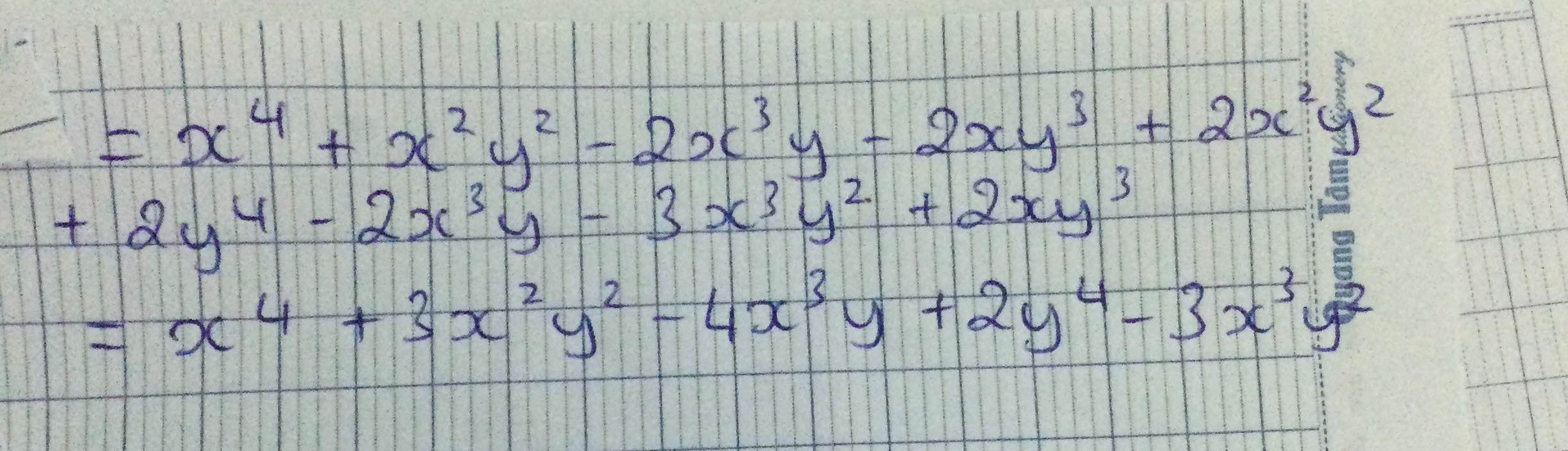\(C=\left(x^2-2xy+y^2\right)\left(x^2+y^2\right)-2x^3y-3x^3y^2+2xy^3\)

\(=\left(x^2+y^2\right)^2-2xy\left(x^2+y^2\right)-xy\left(2x^2+3x^2y+2y^2\right)\)

\(=\left(x^2+y^2\right)^2-xy\left(2x^2+2y^2+2x^2+3x^2y+2y^2\right)\)

\(=\left(x^2+y^2\right)^2-xy\left(4x^2+3x^2y+4y^2\right)\)

\(x^2+2y^2-2xy+x-2y+1=0\)

\(4x^2+8y^2-8xy+4x-8y+4=0\)

\(4x^2-4x\left(2y-1\right)+\left(2y-1\right)^2+8y^2-8y+4-\left(2y-1\right)^2=0\)

\(\left(2x-2y+1\right)^2+\left(4y^2-4y+1\right)+3=0\)

\(\left(2x-2y+1\right)^2+\left(2y-1\right)^2+3=0\) ( vô lí)

=> KL...........

vô lí

Đáp án A

y − 1 x 2 + 2 y − 1 x + 2 y − 1 = 0 1  

Nếu y = 1  thì   x = 1

Nếu y ≠ 1  thì để (1) có nghiệm thì

Δ = 2 y − 1 2 + 4 y − 1 2 y − 1 ≥ 0 ⇔ 2 y − 1 3 − 2 y ≥ 0 ⇔ 1 2 ≤ y ≤ 3 2

⇒ min y = 1 2 ; max y = 3 2 ⇒ min y + max y = 2  

=>x^2-2xy+y^2+y^2+2y+1=0

=>(x-y)^2+(y+1)^2=0

=>x=y=-1

B=-2022-2023=-4045

a: \(\dfrac{\left(x+1\right)}{x^2+2x-3}=\dfrac{\left(x+1\right)}{\left(x+3\right)\cdot\left(x-1\right)}=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+5\right)}{\left(x+3\right)\left(x-1\right)\left(x+2\right)\left(x+5\right)}\)

\(\dfrac{-2x}{x^2+7x+10}=\dfrac{-2x}{\left(x+2\right)\left(x+5\right)}=\dfrac{-2x\left(x+3\right)\left(x-1\right)}{\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x-1\right)}\)

b: \(\dfrac{x-y}{x^2+xy}=\dfrac{x-y}{x\left(x+y\right)}=\dfrac{y^2\left(x-y\right)}{xy^2\left(x+y\right)}\)

\(\dfrac{2x-3y}{xy^2}=\dfrac{\left(2x-3y\right)\left(x+y\right)}{xy^2\left(x+y\right)}\)

c: \(\dfrac{x-2y}{2}=\dfrac{\left(x-2y\right)\left(x-xy\right)}{2\left(x-xy\right)}\)

\(\dfrac{x^2+y^2}{2x-2xy}=\dfrac{x^2+y^2}{2\left(x-xy\right)}\)

\(x^2+2y^2+2xy-14y+49=0\)

\(\Leftrightarrow\left(x+y\right)^2+\left(y-7\right)^2=0\)

Dấu '=' xảy ra khi y=7 và x=-7

\(\left(x+y\right)^2+\left(y-7\right)^2=0\)
\(\Rightarrow x=-7;y=-7\)

Mong cái này giúp được bạn nhé. ☺

\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)

\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)

\(P=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\\ P=2x^2+x-x^3-2x^2+x^3-x+3\\ P=3\left(đfcm\right)\)

\(x^2+2y^2-4x+2y+\dfrac{9}{2}=0\)

\(x^2-4x+4+2y^2+2y+\dfrac{1}{2}=0\)

\(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2=0\)

Vì \(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2\ge0\forall x,y\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\)

\(x^2+2y^2-4x+2y+\dfrac{9}{2}=0\)

=>\(x^2-4x+4+2y^2+2y+\dfrac{1}{2}=0\)

=>\(\left(x-2\right)^2+2\left(y^2+y+\dfrac{1}{4}\right)=0\)

=>\(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2=0\)

mà \(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2>=0\forall x,y\)

nên \(\left\{{}\begin{matrix}x-2=0\\y+\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\)