Cho hình bên: Ax // By
Tính \(\widehat{C}\)
1.Cho hình 16:
a) Cho biết \(Ax//Cy.So\) \(sánh \)\(\widehat{ABC}\) với \(\widehat{A}\) và \(\widehat{C}\)
b) Cho biết \(\widehat{ABC}\)=\(\widehat{A}\) và\(\widehat{C}\) . Chứng tỏ rằng \(Ax//\) Cy
Cho hình vẽ bên, biết Ax//By, góc A bằng 20o, góc B bằng 120o. Tính số đo x (góc C)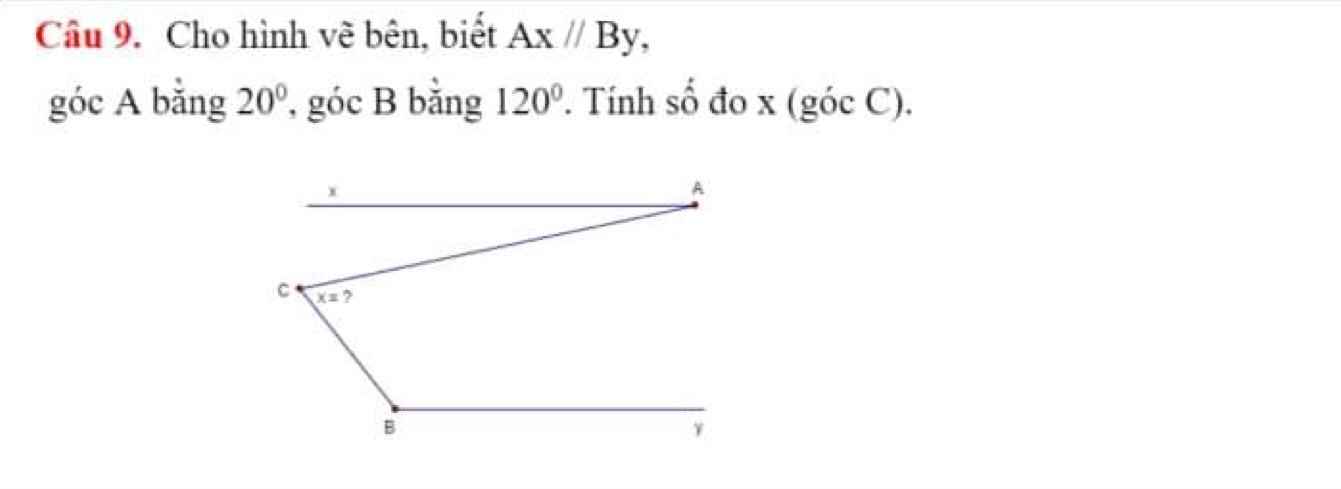
Bài 6: Cho hình vẽ bên. Biết Ax // By, xAB = 120°, BCz = 120°.
a) Tính số đo góc ABy?
b) Các cặp đường thẳng nào song song với nhau ?Vì sao ?
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
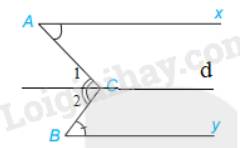
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
cho a,b,c,x,y,z thỏa mãn: ax+by=c, by+cz=a, cz+ax=b, x,y,z khác -1, (a+b+c) khác 0. Tính P=1/(x+1)+1/(y+1)+1/(z+1)
Ta có ax + by = c ; by + cz = a
<=> cz - ax = a - c (1)
mà cz + ax = b (2)
Từ (1) và (2) => \(cz=\frac{a-c+b}{2}\Rightarrow z=\frac{a-c+b}{2c}\Rightarrow z+1=\frac{a+b+c}{2c}\)
=> \(\frac{1}{z+1}=\frac{2c}{a+b+c}\)
Tương tự ta có \(\frac{1}{x+1}=\frac{2a}{a+b+c}\); \(\frac{1}{y+1}=\frac{2b}{a+b+c}\)
=> P = \(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}=\frac{2a}{a+b+c}+\frac{2b}{a+b+c}+\frac{2c}{a+b+c}=2\)
Cho hình vẽ, chứng minh: Ax song song By ( Ax//By )
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
(2,0 điểm) Cho hình vẽ, biết $Cz // Ax;$ $\widehat{C}=30^{\circ} ; \widehat{A C B}=110^{\circ}$.

a) Chứng minh rằng: ${Ax} / / {By}$ và ${Cz} / / {By}$;
b) Tính số đo góc $\widehat{C B y}$;
a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)
A) Ax⊥m(gt);By⊥m(gt) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
Cho a=x2 - yz; b= y2 - zx: c= z2 - xy.
a) Tính tổng ax+by+ cz và tổng a+b+c
b) CMR ax+by+ cz=(x +y + z)(a+b+c)
a: \(ax+by+cz\)
\(=x^3-xyz+y^3-xyz+z^3-xyz\)
\(=x^3+y^3+z^3-3xyz\)
Cho a=x2 - yz; b= y2 - zx: c= z2 - xy.
a) Tính tổng ax+by+ cz và tổng a+b+c
b) CMR ax+by+ cz=(x +y + z)(a+b+c
b: \(ax+by+cz\)
\(=x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3yxz\)
\(=\left(x+y+z\right)\left(x^2+y^2+2xy-xz-yz+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
Cho các số a,b,c,x,y,z t/m:x=by+cz ;y=cz+ax ;z=ax+by và a,b,c khác 0.Tính M=1/1+a+1/1+b+1/1+c