cho tam giác có góc B = góc C Tia phân giác của góc A cắt BC tại D Chứng minh rằng : a) tam giác ADB tam giác ADC b) AB = AC

Những câu hỏi liên quan
Cho tam giác ABC có góc B = góc C . Tia phân giác của góc A cắt BC tại D. Chứng minh rằng BD=DC;AB=AC
cái này dẽ mà chỉ càn chứng minh 2 tam giác có chứa 2 cạnh đó bằng nhau là được
Đúng 0
Bình luận (0)
Xét tam giác ABD và tam giác ACD ta có:
Góc BAD = góc CAD (t/chất tia phân giác)
AD cạnh chung
Góc B = góc C (gt)
=> Tam giác ABD = tam giác ACD (g.c.g)
=> BD = DC (2 cạnh tương ứng)
AB = AC (2 cạnh tương ứng)
Mấy bài này cũng dễ mà, tự động não k đc à?
Đúng 0
Bình luận (0)
THANH NGUYEN làm sai rồi bạn ơi
VÌ cạnh có xen giữa 2 góc đâu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A. Tia phân giác của góc B cắt AC tại D và tia phân giác của góc C cắt AB tại E. a) Chứng minh rằng: EBD D = EC b) Chứng minh rằng: ADE cân c) Chứng minh rằng: ED // BC d) Gọi O là giao điểm của EC và BD. Chứng minh rằng: OBC cân
a: Xét ΔABC có BD là đường phân giác
nên AB/BC=AD/DC
=>AD/DC=AC/BC(1)
Xét ΔABC có CE là đường phân giác
nên AE/EB=AC/BC(2)
Từ (1) và (2) suy ra AD/DC=AE/EB
=>ED//BC
=>\(\widehat{EDB}=\widehat{DBC}\)
mà \(\widehat{DBC}=\widehat{EBD}\)
nên \(\widehat{EDB}=\widehat{EBD}\)
b: Xét ΔABC có DE//BC
nên AE/AB=AD/AC
mà AB=AC
nên AE=AD
hay ΔADE cân tại A
Đúng 1
Bình luận (1)
Cho tam giác ABC có góc A = 600, kẻ tia phân giác của góc B cắt AC ở D, tia phân giác góc C cắt AB ở E. Qua A kẻ đường thẳng song song với CE, đường thẳng này cắt đường thẳng BC tại E. a. Chứng minh rằng góc AFC = CAF b. Chứng minh rằng góc BDC = AEC
Cho tam giác ABC có A = 180°– 3C a) Chứng minh rằng B = 2C. Cho B = 80°, tính số do các góc của tam giác. b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường song song với BC, cắt AB tại D. Chứng minh rằng ED là tia phân giác của góc AEB. Huhu mọi ngừi cố gắng giúp mình nha, thanks nè ❤️❤️❤️
\(a,\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180\) mà \(\widehat{A}=180-3\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=180-\widehat{A}=3C\\ \Rightarrow\widehat{B}=2\widehat{C}\)
Thay \(\widehat{B}=80\Rightarrow\widehat{C}=\dfrac{80}{2}=40\Rightarrow\widehat{A}=180-3\cdot40=60\)
\(b,\) Ta có \(DE//BC\)
\(\Rightarrow\widehat{EBC}=\widehat{DEB}\left(SLT\right)\)
Ta có \(\widehat{AEB}=\widehat{C}+\widehat{EBC}=\widehat{C}+\dfrac{1}{2}\widehat{B}=\widehat{C}+\dfrac{1}{2}\cdot2\widehat{C}=2\widehat{C}=\widehat{B}\)
(vì \(\widehat{AEB}\) là góc ngoài \(\Delta EBC\))
\(\Rightarrow\widehat{AED}+\widehat{DEB}=\widehat{ABE}+\widehat{EBC}\)
Mà \(\widehat{EBC}=\widehat{DEB}\left(cmt\right)\)
\(\Rightarrow\widehat{AED}=\widehat{ABE}\)
Mà \(\widehat{EBC}=\widehat{ABE}\left(GT\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{AED}\)
Vậy \(ED\) là phân giác \(\widehat{AEB}\)
Đúng 2
Bình luận (0)
cho tam giác abc có góc b=góc c. tia phân giác của góc a cắt bc tại d. chứng minh rằng
a)tam giác adb=tam giác adc
b)AB=AC
b ) GÓC B = GÓC C
=> TAM GIÁC ABC CÂN TẠI A
=> AB = AC (ĐPCM)
a) XÉT 2 TAM GIÁC ADB VÀ ADC, CÓ:
AB = AC (THEO CÂU B)
AD LÀ CẠNH CHUNG
GÓC A1 = GÓC A2 (AD LÀ PHÂN GIÁC, GT)
=> TAM GIÁC ADB = ADC (C.G.C) (ĐPCM)
Đúng 0
Bình luận (0)
a) Xét tam giác adb và tam giác adc
ab = ac
góc a1 và góc a2 là cạnh chung
Suy ra tam giác adb = tam giác adc
b) Vì tam giác adb = tam giác adc
Nên AB = AC
Đúng 0
Bình luận (0)
cho tam giác ABC có góc B = góc C . tia phân giác góc A cắt BC tại D .chứng minh rằng AD vuông góc BC và D là trung điểm BC
ΔABC có: \(\widehat{B}=\widehat{C}\)(gt)
=> ΔABC cân tại A
Mà AD là tia phân giác ứng với của \(\widehat{A}\)
=>AD cx là đường cao , cx là đường trung tuyến
=>AD vuông góc với BC
D là trung điểm BC
Đúng 0
Bình luận (0)
Tam giác ABC có góc B bằng góc C (1) nên tam giác ABC cân tại A => AB=AC (2)
Góc DAB= góc DAC (3)
Từ (1)(2)(3) suy ra tam giác DAB=DAC (g.c.g)
=> ADB=ADC=BDC/2=180/2=90 độ
Hay AD vuông góc với BC
tam giác DAB=DAC (g.c.g)
=> DB=DC (2 cạnh tường ứng)
Hay D là trung điểm của BC
Đúng 0
Bình luận (0)
Vì góc B = góc C => tam giác ABC cân tại A
Mà AD là phân giác trong tam giác ABC nên AD cũng là đường cao => AD vuông góc vs BC
Vì ABC cân nên AD cũng là trung tuyến => D là trung điểm BC
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác ABC cân tại A. Tia phân giác của góc B cắt AC tại D và tia phân giác của góc C cắt AB tại E. a) Chứng minh rằng: EBDD EC= b) Chứng minh rằng: ADE cân c) Chứng minh rằng: ED // BC d) Gọi O là giao điểm của EC và BD. Chứng minh rằng: OBC cân
b: Xét ΔABD và ΔACE có
\(\widehat{BAD}\) chung
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
c: Xét ΔABC có
AE/AB=AD/AC
Do đó: DE//BC
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có hai góc bằng nhau.
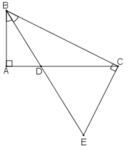
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)
+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)
+) Tam giác ABD vuông tại A nên:
∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)
Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)
+) Tam giác BCE vuông tại C nên:
∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)
Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)
Vậy tam giác CDE có hai góc bằng nhau.
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có ab=3cm ac=4cm a)tính độ dài cạnh bc b) tia phân giác góc b cắt ac tai e vẽ eh vuông góc với bc tai h.chứng minh rằng tam giác abe =tam giác hbe và ab=hb c)tia ba cắt tia he tại d .chứng minh rằng be vuông góc với cd d)kẻ đường thẳng d vuông góc với bc tại b,d cắt tia ca tại m.tia phân giác của góc m cắt bc tại k.chứng minh rằng mk song sonhg với dc
1 ) Cho tam giác ABC có góc B = góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài tại đỉnh A . Chứng minh rằng : Ax//Bc
2 ) Cho tam giác ABC vuông tại A . Vẽ AH vuông góc với BC . Các tia phân giác của các góc BAH và góc C cắt nhau tại K . Chứng minh rằng : AK vuông góc với CK

























