trong mặt phẳng xOy cho 3 điểm A(-1:2) B(4;-2) C(-3;-1)
tìm tọa độ của điểm M để tâm giác BCM vuông cân tại M
Những câu hỏi liên quan
Trên mặt phẳng tọa độ xOy ,Cho 3 điểm: A( 0; 2) ; B(-3;-1) ; C( 2; 4). Chứng minh 3 dierdrm A,B,C thẳng hàng
\(\overrightarrow{AB}=\left(-3;-3\right)=>AB:x+y-2=0=>y=x+2\)
Thay x = 2; y = 4 vào pt đường thẳng AB ta được 4 = 2 + 2 (luôn đúng )
=> điểm C thuộc đường thẳng AB , tương tự điểm B cũng thuộc đường thẳng AB
Vậy suy ra 3 điểm A,B,C thẳng hàng
Trong không gian với hệ tọa độ Descartes Oxyz, cho hai điểm A(3, 2, 1) và
B
-
1
;
4
;
-
3
. Điểm M thuộc mặt phẳng (xOy) sao cho
M
A
-
M
B
lớn nhất là A.
M
-...
Đọc tiếp
Trong không gian với hệ tọa độ Descartes Oxyz, cho hai điểm A(3, 2, 1) và B - 1 ; 4 ; - 3 . Điểm M thuộc mặt phẳng (xOy) sao cho M A - M B lớn nhất là
A. M - 5 ; 1 ; 0
B. M(5, 1, 0)
C. M 5 ; - 1 ; 0
D. M - 5 ; - 1 ; 0
Chọn B.
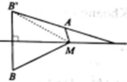
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
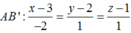
Từ đó tìm được M(5, 1, 0).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa dộ xOy, cho các điểm A(5; 4), B(2: 3) , C(6; 1)
Số đo \(\widehat{BAC}\)bằng ....
Hướng dãn cách giải hộ mình nhé !
Bài 1 : tìm m để 3 điểm A( 2 ; -1 ) , B ( 1 ; 1 ) , C ( 3 ; m+1 ) trong mặt phẳng Oxy thẳng hàng .
Bài 2 : trong mặt phẳng Oxy cho A ( 1; 2 ) , B ( 3 ; 4 ) . tìm điểm M thuộc Ox sao cho MA + MB đạt giá trị nhỏ nhất .
1. Cho góc xOy = 90 độ và điểm A nằm trong góc xOy gọi B và C là 2 điểm thứ tự trên Ox,Oy ( O,A thuộc nửa mặt phẳng bờ BC ) biết tam giác ABC vuông cân tại A. CMR: OA là phân giác góc xOy
Trong mặt phẳng tọa độ Oxy cho 3 điểm A(1; 2), B(3; 4); C(a - 1; b + 2);
Để C là trung điểm của AB thì a = ................
Ta có : Để C là trung điểm của AB thì :
\(\hept{\begin{cases}2\left(a-1\right)=1+3\\2\left(b+2\right)=2+4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=3\\b=1\end{cases}}\)
Đúng 0
Bình luận (0)
trong mặt phẳng oxy cho 3 điểm A(1 4) B(3 -1) C(6 2) không thẳng hàng.Tính khoảng cách từ điểm A đến đường thẳng BC
vecto BC=(3;3)=(1;1)
Phương trình BC là:
1(x-6)+1(y-2)=0
=>x+y-8=0
\(d\left(A;BC\right)=\dfrac{\left|1\cdot1+1\cdot4-8\right|}{\sqrt{1^2+1^2}}=\dfrac{3\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho các điểm A(1; 2), B(-1;-1), C(0; 3),
D(4;-2), E(6; 4); F(1;-1). Trong số các điểm trên, số điểm có tung độ dương là
A. 2. B. 3.
C. 4. D. 5.
Có 3 điểm có tung độ dương (A,C,E)
Đáp án B
Đúng 0
Bình luận (0)
Cho 4 điểm A,B,C,D không thuộc đường thẳng a, trong đó điểm A thuộc 1 nửa mặt phẳng bờ a, còn điểm B,C,D thuộc nửa mặt phẳng kia. Đường thẳng a cắt đoạn thẳng nào trong các đoạn thẳng nửa 2 trong 4 điểm A,B,C,D