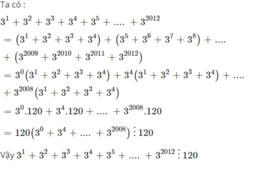Tổng S = 31+32+33+......+32012 có chia hết cho 120 . Vì sao

Những câu hỏi liên quan
Tổng 31 + 32 + 33 + 34 + 35 + … + 32012 có chia hết cho 120 không? Vì sao?
Tổng trên = (31+32012).[(32012-31:1+1] : 2 = 32043 . 31982 : 2 = 42043 . 15991 lẻ
=> tổng trên ko chia hết cho 120
k mk nha
Đúng 0
Bình luận (0)
Tổng trên có 31982 số hạng
Nên tổng trên bằng:(32012+31).31982/2
=32043.15991 là số lẻ ko chia hết cho 120
Tk mình nha bn !
Đúng 0
Bình luận (0)
Tổng 31 + 32 + 33 + 34 + 35 + … + 32012 có chia hết cho 120 không? Vì sao?
các bạn giải chi tiết giúp mình với!
không chia hết cho 120 vì tổng trên là số lẻ nên không chia hết cho một số chẵn
Đúng 0
Bình luận (0)
còn 1 cách nào khác hok bạn? mik hok hỉu một chút
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tổng 31 + 32 + 33 + 34 + 35 + … + 32012 có chia hết cho 120 không? Vì sao?
giúp mk với mai thi òi![]()
Tổng 31 + 32 + 33 + 34 + 35 + … + 32012 không chia hết cho 120 vì tổng trên là một số lẻ, không chia hết cho một số chẵn.
Đúng 0
Bình luận (0)
tổng trên không chia hết cho 120. Vì các số trên có tổng là số lẻ lên không chia hết cho số chẵn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tổng nào chia hết cho 6 vì sao
a, A = 6 +12 + 120 + 60 + 736
B= 24+48+31+120+558
C= 16+33+8+27
a)
Vì dãy A chứa toàn số \(⋮6\)
=> Tổng tất cả các số đều \(⋮6\)
=> \(A⋮6\)
b) Có: \(24;48;120;558⋮6\)
Nhg \(31⋮̸̸6\)
=> B ko chia hết cho 6
c) Có: \(C=16+33+8+27=84⋮6\)
Vậy dãy \(C⋮6\)
cho A = 31 + 32 + 33 + 34 +35 +...... +32012
Chứng minh A chia hết cho "120"
\(A=3+3^2+3^3+...+3^{2012}\\ A=\left(3+3^2+3^3+3^4\right)+...+\left(3^{2009}+3^{2010}+3^{2011}+3^{2012}\right)\\ A=120+...+3^{2008}.120\\ A=120.\left(1+...+3^{2008}\right)⋮120\)
Đúng 1
Bình luận (2)
\(=\left(3+3^2+3^3+3^4\right)+...+3^{2008}\left(3+3^2+3^3+3^4\right)\)
\(=120+...+3^{2008}.120=120\left(1+...+3^{2008}\right)⋮120\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Chứng minh: B = 31 + 32 + 33 + 34 + … + 32010 chia hết cho 4.
b) Chứng minh: C = 51 + 52 + 53 + 54 + … + 52010 chia hết cho 31.
c) Cho S=17+52+53+54+ ... +52010 . Tìm số dư khi chia S cho 31.
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
Đúng 3
Bình luận (0)
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
Đúng 2
Bình luận (0)
a)S=3+31+32+33+34+......+320
chứng minh chia hết cho 20
Cho B = 3 + 32 + 33 + …… + 360. Hãy cho biết B có chia hết cho 13 không? Vì sao?
\(B=3+3^2+3^3+...+3^{60}\)
\(=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
Đúng 2
Bình luận (0)
Cho B = 3+32+33+...+360. hãy cho biết B có chia hết cho 13 không? vì sao?
Số số hạng của B:
60 - 1 + 1 = 60 (số)
Do 60 ⋮ 3 nên ta có thể nhóm các số hạng của B thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
B = (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3⁵⁸ + 3⁵⁹ + 3⁶⁰)
= 3.(1 + 3 + 3²) + 3⁴.(1 + 3 + 3²) + ... + 3⁵⁸.(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3⁵⁸.13
= 13.(3 + 3⁴ + ... + 3⁵⁸) ⋮ 13
Vậy B ⋮ 13
Đúng 2
Bình luận (0)
Bài 8. Cho A = 3 + 32 + 33 + ... + 32020 . Hỏi A có chia hết cho 4 không? Vì sao?
\(A=3+3^2+3^3+...+3^{2020}=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2019}.\left(1+3\right)=\left(1+3\right)\left(3+3^3+...+3^{2019}\right)=4.\left(3+3^3+...+3^{2019}\right)⋮4\)
Đúng 1
Bình luận (0)
A=3 + 32 + 33 + ... + 32020 =3 (1 + 3) + 33 (1 + 3) + ... + 32019 . (1 + 3)
=(1 + 3)(3 + 33+...+32019)=4 . ( 3 + 33+ ... + 32019) ⋮ 4
Đúng 0
Bình luận (0)