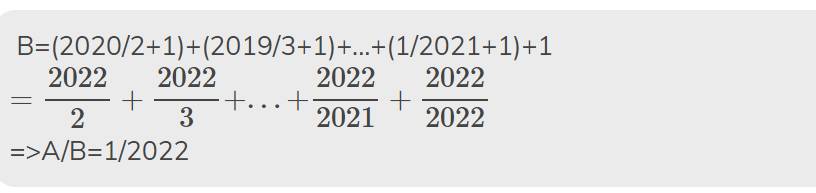2:

a: Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{24}{9}=\dfrac{8}{3}\)

=>x=16/3; y=8; z=32/3

A=3x+2y-6z

=3*16/3+2*8-6*32/3

=16+16-64

=-32

b: Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y+z}{5-6+7}=\dfrac{6\sqrt{2}}{6}=\sqrt{2}\)

=>x=5căn 2; y=6căn 2; y=7căn 2

B=xy-yz

=y(x-z)

=6căn 2(5căn 2-7căn 2)

=-6căn 2*2căn 2

=-24

bài 1 a)áp dụng dãy tỉ số bằng nhau ta có:\(\dfrac{a+b+c}{3+4+5}\)=\(\dfrac{24}{12}\)=2

a=2.3=6 ; b=2.4=8 ;c=2.5=10

M=ab+bc+ac=6.8+8.10+6.10=48+80+60=188

"nhưng bài còn lại làm tương tự"

\(\Leftrightarrow12a^2-4b^2=3a^2+3b^2\)

\(\Leftrightarrow9a^2=7b^2\)

\(\Leftrightarrow\dfrac{a^2}{b^2}=\dfrac{7}{9}\)

hay \(\dfrac{a}{b}\in\left\{\dfrac{\sqrt{7}}{3};-\dfrac{\sqrt{7}}{3}\right\}\)

\(\dfrac{3a^2-b^2}{a^2+b^2}=\dfrac{3}{4}\)

\(\Leftrightarrow4.\left(3a^2-b^2\right)=3\left(a^2+b^2\right)\)

\(\Leftrightarrow12a^2-4b^2=3a^2+3b^2\)

\(\Leftrightarrow12a^2-3a^2=3b^2+4b^2\)

\(\Leftrightarrow9a^2=7b^2\)

\(\Leftrightarrow\dfrac{a^2}{b^2}=\dfrac{7}{9}\)

\(\text{hoặc }\dfrac{a}{b}=\pm\dfrac{\sqrt{7}}{3}\)

Ta có \(A=\dfrac{1}{2}+\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+\left(\dfrac{3}{2}\right)^4+...+\left(\dfrac{3}{2}\right)^{2021}\left(1\right)\)

\(\Rightarrow\dfrac{3}{2}A=\dfrac{3}{4}+\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+\left(\dfrac{3}{2}\right)^4+...+\left(\dfrac{3}{2}\right)^{2013}\left(2\right)\)

Lấy (2) - (1) ta được:

\(\dfrac{3}{2}A-A=\left(\dfrac{3}{2}\right)^{2013}+\dfrac{3}{4}-\dfrac{1}{2}-\dfrac{3}{2}\)

\(\dfrac{1}{2}A=\left(\dfrac{3}{2}\right)^{2013}+\dfrac{1}{4}\Rightarrow A=\dfrac{3^{2013}}{2^{2012}}+\dfrac{1}{2}\)

Vậy \(B-A=\dfrac{3^{2013}}{2^{2014}}-\dfrac{3^{2013}}{2^{2012}}+\dfrac{5}{2}\)

Ai trả lời đi please

A= 1+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)

= \(\dfrac{2015}{2015}\)+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)

= 2015.(\(\dfrac{1}{2015}\)+\(\dfrac{1}{2014}\)+\(\dfrac{1}{2013}\)+...+\(\dfrac{1}{2}\))=2015.B

\(\Rightarrow\) \(\dfrac{A}{B}\)=2015

Đặt \(\dfrac{a}{b^2}=\dfrac{b^2}{c^3}=\dfrac{c^3}{a^4}=k\)

\(\Rightarrow\left\{{}\begin{matrix}a=k.b^2\\b^2=k.c^3\\c^3=k.a^4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=k.k.c^3=k^2c^3\\c^3=k.a^4\end{matrix}\right.\)

\(\Rightarrow a=k^2.k.a^4\)

\(\Rightarrow a=k^3a^4\)

\(\Rightarrow\left(ka\right)^3=1\)

\(\Rightarrow ka=1\)

\(\Rightarrow a=\dfrac{1}{k}\) (1)

Thế vào \(c^3=k.a^4\Rightarrow c^3=k.\dfrac{1}{k^4}=\dfrac{1}{k^3}\)

\(\Rightarrow c=\dfrac{1}{k}\) (2)

Thế vào \(b^2=kc^3\Rightarrow b^2=k.\dfrac{1}{k^3}=\dfrac{1}{k^2}\)

\(\Rightarrow b=\dfrac{1}{k}\) hoặc \(b=-\dfrac{1}{k}\) (3)

(1);(2);(3) \(\Rightarrow\left[{}\begin{matrix}a=b=c\\a=c=-b\end{matrix}\right.\)

TH1: \(a=b=c\)

\(\Rightarrow P=\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)=2.2.2=8\)

Th2: \(a=c=-b\)

\(\Rightarrow P=\left(1+\dfrac{-b}{b}\right)\left(1+\dfrac{b}{-b}\right)\left(1+\dfrac{-b}{-b}\right)=0.0.2=0\)

\(B=\dfrac{1}{49}+\dfrac{2}{48}+\dfrac{3}{47}+...+\dfrac{48}{2}+\dfrac{49}{1}\)

\(B=\left(\dfrac{1}{49}+1\right)+\left(\dfrac{2}{48}+1\right)+\left(\dfrac{3}{47}+1\right)+...+\left(\dfrac{48}{2}+1\right)+\dfrac{49}{1}\)

\(B=\left(\dfrac{50}{49}+\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}\right)+1\)

\(B=\dfrac{50}{50}+\dfrac{50}{49}+\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}\)

\(B=50\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+...+\dfrac{1}{2}\right)\)

\(\Rightarrow\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{49}+\dfrac{1}{50}}{50\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+...+\dfrac{1}{2}\right)}=\dfrac{1}{50}\)

`A=(8 2/7-4 2/7)-3 4/9`

`=8+2/7-4-2/7-3-4/9`

`=4-3-4/9`

`=1-4/9=5/9`

`B=(10 2/9-6 2/9)+2 3/5`

`=10+2/9-6-2/9+2+3/5`

`=4+2+3/5`

`=6+3/5=33/5`

Bài 2:

`a)5 1/2*3 1/4`

`=11/2*13/4`

`=143/8`

`b)6 1/3:4 2/9`

`=19/3:38/9`

`=19/3*9/38=3/2`

`c)4 3/7*2`

`=31/7*2`

`=62/7`

Bài 1:

\(A=\left(8\dfrac{2}{7}-4\dfrac{2}{7}\right)-3\dfrac{4}{9}\) 

\(A=\left(\dfrac{58}{7}-\dfrac{30}{7}\right)-\dfrac{31}{9}\) 

\(A=4-\dfrac{31}{9}\) 

\(A=\dfrac{5}{9}\) 

\(B=\left(10\dfrac{2}{9}-6\dfrac{2}{9}\right)+2\dfrac{3}{5}\) 

\(B=\left(\dfrac{92}{9}-\dfrac{56}{9}\right)+\dfrac{13}{5}\) 

\(B=4+\dfrac{13}{5}\) 

\(B=\dfrac{33}{5}\)

Bài 2:

a) \(5\dfrac{1}{2}.3\dfrac{1}{4}=\dfrac{11}{2}.\dfrac{13}{4}=\dfrac{11.13}{2.4}=\dfrac{143}{8}\) 

b) \(6\dfrac{1}{3}:4\dfrac{2}{9}=\dfrac{19}{3}:\dfrac{38}{9}=\dfrac{19}{3}.\dfrac{9}{38}=\dfrac{3}{2}\) 

c) \(4\dfrac{3}{7}.2=\dfrac{31}{7}.2=\dfrac{31.2}{7}=\dfrac{62}{7}\)

\(B=\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)+1\)

\(=\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}+\dfrac{2022}{2022}\)

=2022(1/2+1/3+...+1/2021+1/2022)

=>B/A=2022