Tìm min A và B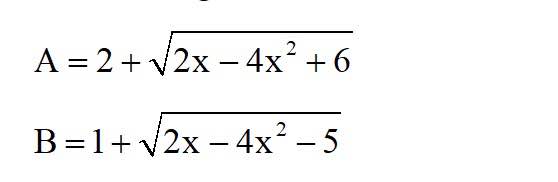

Những câu hỏi liên quan
+) Tìm min
\(E=\dfrac{1+\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{z}}{xy+yz+zx}\)
+) Tìm max và min
\(F=\dfrac{a-b}{c}+\dfrac{b-c}{a}+\dfrac{c-a}{b}\)
Trong đó a,b,c>0 và \(min\left\{a,b,c\right\}\ge\dfrac{1}{4}max\left\{a,b,c\right\}\)
Cho 2 số thực dương a và b thỏa mãn
a, sin (2 - 2ab) - sin (a + b) = 2a + a+ b - 2
Tìm Min của S = a + 2b
b, cos (x + y + 1) + 3 = cos(3xy) + 9xy - 3x - 3y
Tìm Min của S = xy + 2x
Cho a,b >0 và a+2b=3. Tìm min P=\(a^2+b^2\)
Cho a,b > 0 và a + b ≤ 4. Tìm Min P = 4/ a2 + b2 + 3/ab
\(P=\dfrac{4}{a^2+b^2}+\dfrac{3}{ab}\)
Áp dụng BĐT Bunhiacopxki ta có:
\(\left(\dfrac{4}{a^2+b^2}+\dfrac{3}{ab}\right)\left[4\left(a^2+b^2\right)+12ab\right]\ge\left[\sqrt{\dfrac{4}{a^2+b^2}.4\left(a^2+b^2\right)}+\sqrt{\dfrac{3}{ab}.12ab}\right]^2=100\)
\(\Rightarrow P\ge\dfrac{100}{4\left(a^2+b^2\right)+12ab}=\dfrac{100}{4\left(a+b\right)^2+4ab}=\dfrac{25}{\left(a+b\right)^2+ab}\)
\(\Rightarrow P\ge\dfrac{25}{4^2+ab}=\dfrac{25}{16+ab}\) (vì \(a+b\le4\)).
Mặt khác ta có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\le\dfrac{4^2}{4}=4\)
\(\Rightarrow P\ge\dfrac{25}{16+4}=\dfrac{5}{4}\)
Dấu "=" xảy ra khi \(a=b=2\).
Vậy \(MinP=\dfrac{5}{4}\), đạt tại \(a=b=2\)
Đúng 1
Bình luận (0)
hãy giải bài toán bằng 2 phương pháp sơ đồ khối và liệt kê cho bài toán sau nhập dãy số gồm 4 số a,b,c,d tìm Min của 4 số a,b,c,d và đưa ra kết quả Min
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
int main()
{
cin>>a>>b>>c>>d;
cout<<min(a,min(b,min(c,d)));
return 0;
}
Đúng 0
Bình luận (0)
Cho a,b> 0 và ab =1.Tìm Min P=\(\dfrac{a^3}{1+b}\) + \(\dfrac{b^3}{1+a}\)
\(\left(a+b\right)^2\ge4ab=4\Rightarrow a+b\ge2\)
\(P=\dfrac{a^4}{a+ab}+\dfrac{b^4}{b+ab}\ge\dfrac{\left(a^2+b^2\right)^2}{a+b+2ab}=\dfrac{\left(a^2+b^2\right)\left(a^2+b^2\right)}{a+b+2}\)
\(\ge\dfrac{\dfrac{1}{2}\left(a+b\right)^2.2ab}{a+b+2}=\dfrac{\left(a+b\right)^2}{a+b+2}=\dfrac{\dfrac{1}{4}\left(a+b\right)^2+\dfrac{3}{4}\left(a+b\right)^2}{a+b+2}\)
\(\ge\dfrac{\dfrac{1}{4}\left(a+b\right)^2+3ab}{a+b+2}=\dfrac{\dfrac{1}{4}\left(a+b\right)^2+1+2}{a+b+2}\)
\(\ge\dfrac{2\sqrt{\dfrac{1}{4}\left(a+b\right)^2.1}+2}{a+b+2}=\dfrac{a+b+2}{a+b+2}=1\)
Dấu = xảy ra khi \(a=b=1\)
Đúng 0
Bình luận (0)
cho a,b,c>0 và abc=1/(a+b+c). Tìm min P=(a+b)(a+c)
Ta có :
\(abc=\frac{1}{a+b+c}\)
\(\Rightarrow abc.\left(a+b+c\right)=1\)
Lai có : \(P=\left(a+b\right)\left(a+c\right)\)
\(=a^2+ab+bc+ac\)
\(=a.\left(a+b+c\right)+bc\)
Áp dụng BĐT AM - GM ta có :
P= \(a\left(a+b+c\right)+bc\ge2\sqrt{a.\left(a+b+c\right).bc}=2\sqrt{1}=2\)
Dấu " = " xảy ra \(\Leftrightarrow a.\left(a+b+c\right)=bc\)
cho a+b+c=5.tìm min của A=a^2+b^2+c^2
Và tìm max của B=ab+bc+bc
*) Tìm GTNN của \(A=a^2+b^2+c^2\)
Ta có :\(\left(1^2+1^2+1^2\right)\left(a^2+b^2+c^2\right)\ge\left(a.1+b.1+c.1\right)^2\)(Bunhiacopxki)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Leftrightarrow a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=\frac{25}{3}\)
*) Tìm GTLN của \(B=ac+bc+ac\)
Ta có \(a^2+b^2+c^2\ge ab+ac+bc\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge3ab+3ac+3bc\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+ac+bc\right)\)
\(\Rightarrow ab+bc+ac\le\frac{\left(a+b+c\right)^2}{3}=\frac{25}{3}\)
Đúng 0
Bình luận (0)
Cho a, b > 0 và a+b=1 tìm Min P = 1/a^3 +b^3 +1/ab


















