Cho hcn ABCD, E là điểm tùy ý trên cạnh AB. C/m SABCD = 2SEDC

Những câu hỏi liên quan
Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.
Chứng minh rằng: S A B C D = 2 S E C D
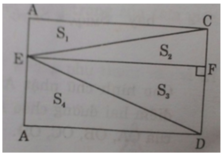
Kẻ EF ⊥ CD ⇒ AC // EF // AD
Xét ΔBCE và ΔFEC có:
(CAE) = (CFE) = 90o
(BCE) = (CEF) (Hai góc so le trong)
CE chung
⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)
tương tự ΔAED=ΔFDE.
Do đó (theo hình vẽ):
S1 = S2 và S3 = S4
⇒ S2 + S3 = S1 + S4 = (1/2)SABCD
Hay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.
Đúng 0
Bình luận (0)
8. cho hcn ABCD đươngf chéo AC và BD cắt nhau tai O . Lấy P là 1 điểm tùy ý trên OB .Gọi M là điểm đx vs C qua P . từ M kẻ ME vuông góc vs đường thẳng AD ( E ∈ AD), kẻ MF vuông goác vs đường thẳng AB (F ∈ AB )
a) cmr AEMF là hcn
b) cmr AMBD là hình thang
c) cm E,F,P thẳng hàng
d) xác định vị trí của P để AMBD là hình thang cân
Chưa ra câu c ^^
a/ Xét tứ giác AEMF có
\(\widehat{EAF}=\widehat{AEM}=\widehat{AFM}=90^o\)
=> Tứ giác AEMF là hcn
b/ Xét t/g AMC có OP là đường trung bình
=> OP // AM
=> BD // AM
=> Tứ giác AMBD là hình thang
d/ Để hình thang AMBD là htc thì AD = BM
=> BM = BC
=> t/g BMC cân tại B có BP là đương trung tuyến
=> CP ⊥ BP tại P
Đúng 1
Bình luận (0)
Cho HCN ABCD (AB > BC).Lấy điểm M tùy ý trên cạnh AB ( M # A và B ) .Đường thẳng DM cắt AC ở K và cắt đường thẳng BC
a.Chứng minh KD mũ 2 =KM*KN
Cho Δ ABC. Lấy điểm M tùy ý trên cạnh BC. Lấy N tùy ý trên cạnh AM. Đường thẳngDE // BC (D ∈ AB, E ∈ AC). Gọi P là giao điểm của DM và BN và Q là giao điểm của CN và EM.Chứng minh rằng: PQ // BC.
Đọc tiếp
Cho Δ ABC. Lấy điểm M tùy ý trên cạnh BC. Lấy N tùy ý trên cạnh AM. Đường thẳng
DE // BC (D ∈ AB, E ∈ AC). Gọi P là giao điểm của DM và BN và Q là giao điểm của CN và EM.
Chứng minh rằng: PQ // BC.
Xét ΔPDN và ΔPMB có
góc PDN=góc PMB
góc DPN=góc MPB
=>ΔPDN đồng dạng với ΔPMB
=>PD/PM=DN/MB=AN/AM
Xét ΔQNE và ΔQCM có
góc QNE=góc QCM
góc NQE=góc CQM
=>ΔQNE đồng dạng với ΔQCM
=>QN/QC=NE/CM=QE/QM=AN/AM
=>QE/QM=DP/PM
=>MP/PD=MQ/QE
=>PQ//DE
=>PQ//BC
Đúng 2
Bình luận (1)
Cho HCN ABCD đường chéo AC và BD cắt nhau tại O.Lấy P là 1 điểm tùy ý trên OB.Gọi M là điểm đối xứng với C qua P. Từ M kẻ ME vuông góc với đường thẳng AB (F thuộc AB)
a) Chứng minh rằng AEFM là HCN
b) Chứng minh rằng AMBD là hình thang
c) Chứng minh E,F,P thẳng hàng
d) Xác định vị trí của P để AMBD là hình thang cân
Cho hình vuông ABCD ,E là điểm tùy ý trên cạnh BC . AE cắt CD tại F,DE cắt AB tại K . Chứng minh rằng BF vuông góc CK
1. cho hình chữ nhật ABCD, E là điểm tùy ý trên cạnh AB. chứng minh SABCD = 2.SEDC
mọi người giúp nhé!!!
Cho hình chóp SABCD có đáy ABCD là tứ giác lồi. Gọi M, N là trung điểm SB, SD. Trên dường chéo AC ta lấy điểm K tùy ý. Tìm thiết diện của hình chóp cắt bởi (KMN).
Cho hcn ABCD, gọi O là giao điểm hai đường chéo. Lấy M tùy ý trên CD, OM cắt AB tại N.
a) cm M đx N qua O
b) dựng NF// AC( F thuộc BC) và ME// AC (E thuộc AD) . Cm NFME là hbh
c) cm MN, EF, AC, BD cắt nhau tại O
Cho hình vuông ABCD cạnh a. M là 1 điểm tùy ý trên đường chéo BD. Kẻ ME vuông góc với AB, MF vuông góc với AD ( E thuộc AB, F thuộc AD).
1.Chứng minh rằng: DE = CF
2.Chứng minh rằng DE, BF, CM đồng quy.
3.Xác định vị trí của M trên cạnh BD để diện tích của AEMF lớn nhất
Xem chi tiết


















