Trên AB lấy trung điểm M, kẻ MN vuông góc với AL ( N thuộc AC)

Qua C kẻ CQ vuông góc với AL tại E, cắt AB tại Q

Xét  \(\Delta CLE\) và   \(\Delta CQB\) có:

    \(\widehat{CEL}=\widehat{CBQ}=90^0\)

    \(\widehat{BCQ}\) chung

suy ra:   \(\Delta CLE~\Delta CQB\) (g.g)

\(\Rightarrow\)\(\widehat{CLE}=\widehat{CQB}\)

mà   \(\widehat{CLE}=\widehat{BLA}\) (đối đỉnh)

suy ra:  \(\widehat{BLA}=\widehat{BQC}\)   

Xét  \(\Delta ABL\)và    \(\Delta CBQ\)có:

    \(\widehat{ABL}=\widehat{CBQ}=90^0\)

    \(AB=AC\) (gt)

   \(\widehat{BAL}=\widehat{BCQ}\)  (do cùng phụ với 2 góc bằng nhau)

suy ra:   \(\Delta ABL=\Delta CBQ\) (g.c.g)

suy ra:   \(BL=BQ\)

mà  \(BL=BM=AM\)

\(\Rightarrow\)\(AM=MB=MQ\)

mà   \(MN//BP//QC\)  (cùng vuông góc với AL)

\(\Rightarrow\)\(AN=NP=PC\)

\(\Rightarrow\)\(AC=3CP\)

\(\Rightarrow\)\(AC=3\sqrt{2}\)

Áp dụng định lý Pytago vào tam giác vuông ABC ta có:

      \(AC^2=AB^2+BC^2\)

\(\Leftrightarrow\)\(AC^2=2AB^2\)  (do AB = BC)

\(\Leftrightarrow\)\(AB^2=\frac{AC^2}{2}\)

\(\Leftrightarrow\)\(AB^2=9\)

\(\Leftrightarrow\)\(AB=3\)

Vậy..

p/s: tham khảo nhé

Thật tốt, 14 năm ms gặp 1 người ... như bạn )

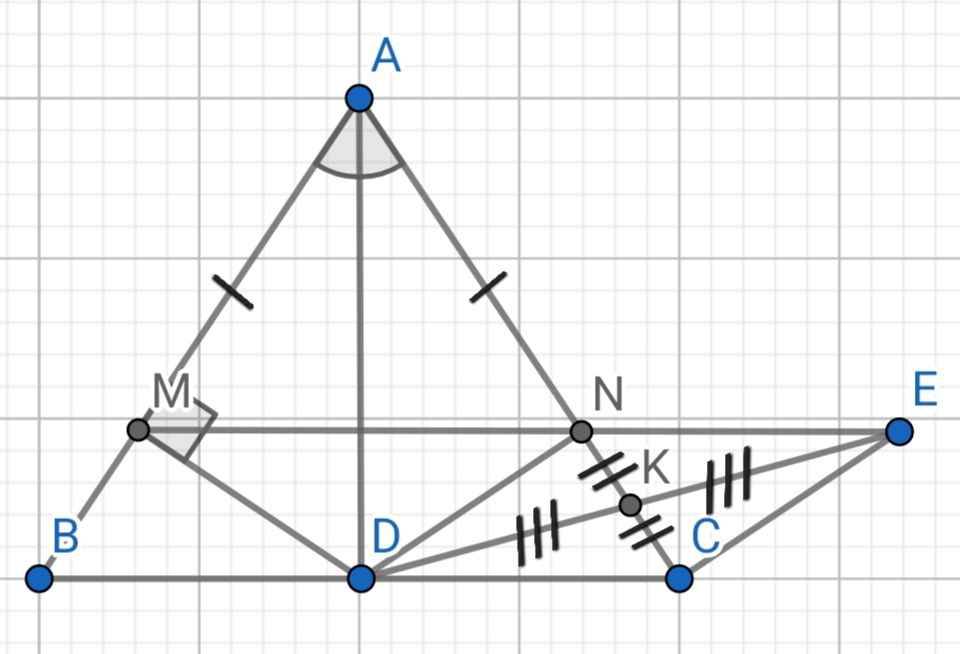 a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ BD = CD

⇒ D là trung điểm của BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

b) Sửa đề: Chứng minh ∆ADM = ∆ADN

Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)

⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)

⇒ DN ⊥ AN

⇒ DN ⊥ AC

d) Do K là trung điểm của CN (gt)

⇒ CK = KN

Xét ∆DKC và ∆EKN có:

CK = KN (cmt)

∠DKC = ∠EKN (đối đỉnh)

KD = KE (gt)

⇒ ∆DKC = ∆EKN (c-g-c)

⇒ ∠KDC = ∠KEN (hai góc tương ứng)

Mà ∠KDC và ∠KEN là hai góc so le trong

⇒ EN // CD

⇒ EN // BC (3)

∆AMN có:

AM = AN (gt)

⇒ ∆AMN cân tại A

⇒ ∠AMN = (180⁰ - ∠MAN) : 2

= (180⁰ - ∠BAC) : 2 (4)

∆ABC cân tại A (gt)

⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)

Từ (4) và (5) ⇒ ∠AMN = ∠ABC

Mà ∠AMN và ∠ABC là hai góc đồng vị

⇒ MN // BC (6)

Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

bn cho nhìu wá

@Hoàng Thị Tuyết Nhung bạn làm giúp mình câu 1 thôi nha

a: Xét ΔCMN và ΔAMB có 

MC=MA

\(\widehat{CMN}=\widehat{AMB}\)

MN=MB

Do đó: ΔCMN=ΔAMB

Suy ra: \(\widehat{MCN}=\widehat{MAB}\) và CN=AB

hay CN\(\perp\)AC

bạn nào giúp mk vẽ hình đc không

Xét ΔADE và ΔABC có :
AD = AB (gt)

góc DAE =góc BAC = 90 độ
AE = AC (gt)
Do đó : ΔADE = ΔABC(c − g − c)
⇒ DE = BC ( hai cạnh tương ứng )
b.
Ta có :
góc ADE =góc CDN ( hai góc đối đỉnh )
góc C= góc E
( vì ΔADE = ΔABC )
⇒ góc N = góc A 90đọ
Hay DE ⊥ BC
Vậy DE ⊥ BC

CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn

tự kẻ hình :

xét tam giác ADH và tam giác ABH có : AH chung

góc AHD = góc AHB = 90 do AH là đường cao (gt)

HD = HB (gt)

=> tam giác AHD = tam giác AHB (2cgv)

=> AdD = AB (đn)

=> tam giác AHB cân (đn)     (1)

tam giác ABC vuông tại A (gt) => góc ABC + góc ACB = 90 (đl)

                                                     mà góc ACB = 30 (gt)

=> góc ABC = 60     (2)

(1)(2) => tam giác ADB đều (đl)

rồ à mấy bọn điên

bạn thiên đừng đăng linh tinh nha

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có

AB=AD

AC=AE

Do đó: ΔABC=ΔADE

b: Xét ΔAMD và ΔANB có

AM=AN

MD=NB

AD=AB

Do đó: ΔAMD=ΔANB