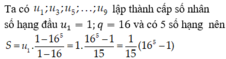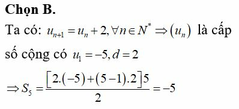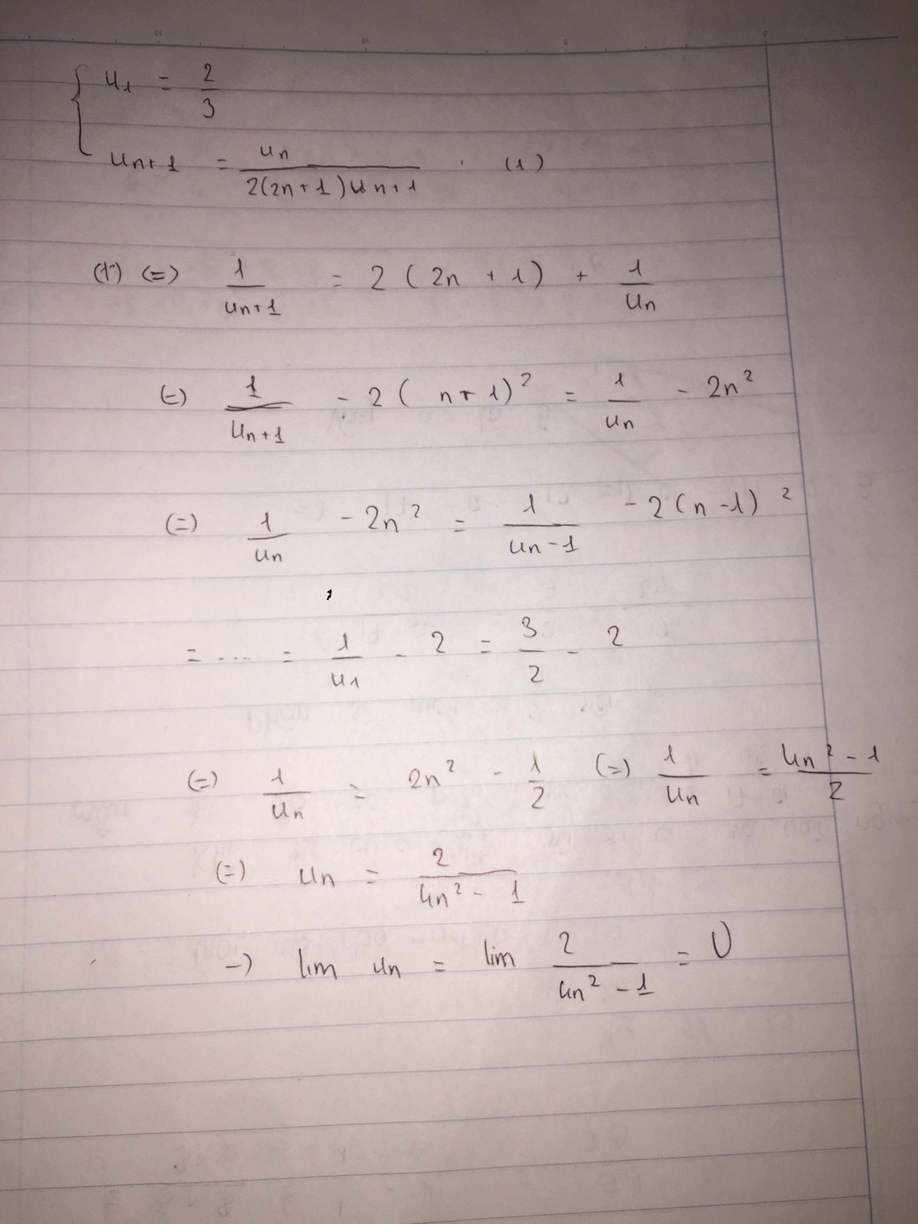Cho dãy số un = 3 - 2n . Tính tổng S50 = u1 + u2 +...+ u50

Những câu hỏi liên quan
Cho dãy số
u
n
biết
u
1
1
u
n
+
1
u
n...
Đọc tiếp
Cho dãy số u n biết u 1 = 1 u n + 1 = u n + 2 n − 1 ∀ n ∈ ℕ * . Tính số hạng u 50
A. 4024
B. 2404
C. 2240
D. 202
Đáp án B
u 2 = u 1 + 1 ; u 3 = u 2 + 3 = u 1 + 1 + 3 ; u 4 = u 3 + 5 = u 1 + 1 + 3 + 5 ; ... ; u 50 = u 1 + 1 + 3 + 5 + ... + 2.49 − 1 = 1 + 1 + 3 + 5 + ... + 97 = 1 + 1 + 97 .49 2 = 2402
Đúng 0
Bình luận (0)
1) cho dãy số (un)(��) được xác định bởi unn^2-1�3�−1a) Tính u1,u2,u3,u4b) 99 là số hạng thứ mấy của dãy2) cho dãy số (un)(��) được xác định bởi u_ndfrac{2n-1}{n+1}a) Tính u1,u2,u3,u4b) dfrac{13}{7} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Đúng 0
Bình luận (0)
Cho dãy số
u
n
với
u
n
4
n
-
1
. Tính tổng
S
u
1
+
u
2
+
u
3...
Đọc tiếp
Cho dãy số u n với u n = 4 n - 1 . Tính tổng S = u 1 + u 2 + u 3 + . . . + u 9
A. S = 1 15 6 5 - 1
B. S = 1 15 8 5 - 1
C. S = 1 2 16 5 - 1
D. S = 1 15 16 5 - 1
cho dãy số (Un) xác định bơi U1=1,U2=-2,U3=3, Un+3=2Un+2- 3Un+1 +Un -2 (n>=1)
tính tổng S=U1+2U2+3U3+...+20U20
Ai gioi toan CASIO ko ak? Giup mik vs
3.2.Cho dãy số u1;u2;u3;...;un;Biết u1= 25 ; u2=u1+121;u3=u1+u2+441;u4=u1+u2+u3+1225;
u5= u1+u2+u3+u4+2809;...
a)Viết quy trình bấm phím liên tục tính un
b)Tính U25;u50
 Toshiro Kiyoshi34GP
Toshiro Kiyoshi34GP
 Nguyễn Huy Tú30GP
Nguyễn Huy Tú30GP
 Hồng Phúc Nguyễn24GP
Hồng Phúc Nguyễn24GP
 Akai Haruma21GP
Akai Haruma21GP
 nguyen van tuan19GP
nguyen van tuan19GP
 T.Thùy Ninh19GP
T.Thùy Ninh19GP
 Xuân Tuấn Trịnh11GP
Xuân Tuấn Trịnh11GP
 Nguyen Ngoc Anh Linh10GP
Nguyen Ngoc Anh Linh10GP
 Nguyen Bao Linh9GP
Nguyen Bao Linh9GP
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
có
u
1
-
5
,
u
n
+
1
u
n...
Đọc tiếp
Cho dãy số ( u n ) có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24
Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
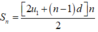
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
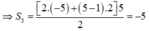
Đúng 0
Bình luận (0)
Cho dãy số
u
n
có
u
1
-
5
,
u
n
+
1
u
n
+
2
,
n
∈
N
*
.
Tổng
S
5
u
1...
Đọc tiếp
Cho dãy số u n có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24
Cho dãy số
u
n
với
u
n
1
2
n
+
1
,
∀
n
∈
N
*
. Tổng
S
2019
u
1
+
u
2
+
.
....
Đọc tiếp
Cho dãy số u n với u n = 1 2 n + 1 , ∀ n ∈ N * . Tổng S 2019 = u 1 + u 2 + . . . + u 2019 bằng
A. 2020 - 1 2 2019
B. 2019 - 1 2 2019
C. 2019 + 1 2 2019
D. 2020 + 1 2 2019
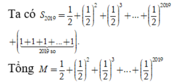 là tổng 2019 số hạng đầu tiên của một cấp số nhân với số hạng đầu
u
1
=
1
2
, công bội q=
1
2
là tổng 2019 số hạng đầu tiên của một cấp số nhân với số hạng đầu
u
1
=
1
2
, công bội q=
1
2
Do đó
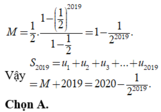
Đúng 0
Bình luận (0)
Cho dãy số (un) thỏa mãn u1 = \(\dfrac{2}{3}\) và un+1 = \(\dfrac{u_n}{2\left(2n+1\right)u_n+1}\left(n\ge1\right)\). Tìm số hạng tổng quát un của dãy. Tính lim un