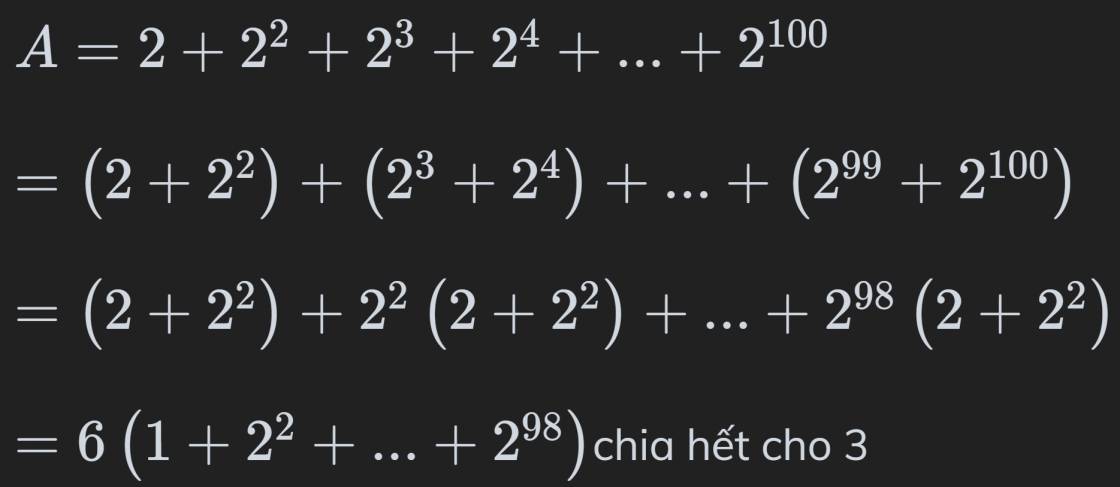0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)

\(b,S6=1-5^{100}\\ 1-S6=5^{100}\) 

=> 5¹⁰⁰ chia 6 du 1

e đang cần gấp, có ai đến giúp e ko?

\(S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ a,S=5^0.\left(1-5\right)+5^2.\left(1-5\right)+...+5^{98}.\left(1-5\right)=-4.\left(5^0+5^2+5^4+...+5^{98}\right)\)

Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip

#@₫!%&@^@₫@₫=_++_×%@%@&@@@@=@

Bài 1:

a: \(S=1-5+5^2-5^3+...+5^{98}-5^{99}\)

=>\(5S=5-5^2+5^3-5^4+...+5^{99}-5^{100}\)

=>\(6S=5-5^2+5^3-5^4+...+5^{99}-5^{100}+1-5+5^2-5^3+...+5^{98}-5^{99}\)

=>\(6S=-5^{100}+1\)

=>\(S=\dfrac{-5^{100}+1}{6}\)

b: S=1-5+5²-5³+...+5⁹⁸-5⁹⁹ là số nguyên

=>\(\dfrac{-5^{100}+1}{6}\in Z\)

=>\(-5^{100}+1⋮6\)

=>\(5^{100}-1⋮6\)

=>\(5^{100}\) chia 6 dư 1

Lời giải:
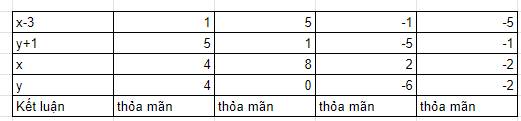
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:

b.

$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$

$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$

$=2+24+(1+5)(5^2+5^4+...+5^{98}$

$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$

$\Rightarrow A$ chia $6$ dư $2$.

\(\frac{a}{b}=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{100}\)

\(\frac{a}{b}=\left(\frac{1}{51}+\frac{1}{100}\right)+\left(\frac{1}{52}+\frac{1}{99}\right)+...+\left(\frac{1}{75}+\frac{1}{76}\right)\)

\(\frac{a}{b}=\frac{151}{51.100}+\frac{151}{50.99}+...+\frac{151}{75.76}\)

Chọn mẫu chung = 51.52.53...100

Gọi các thừa số phụ lần lượt là: k₁; k₂; ...; k₂₅

=> \(\frac{a}{b}=\frac{151.\left(k_1+k_2+...+k_{25}\right)}{51.52...100}\)

Do 151 là số nguyên tố mà tích 51.52...100 không chứa thừa số 151 => 51.52....100 không chia hết cho 151

=> đến khi phân số a/b tối giản thì a vẫn chia hết cho 151 (đpcm)

Mik rút gọn cho bn nha

\(\frac{a}{b}=\frac{1}{51.100}+\frac{1}{52.99}+..........+\frac{1}{100.51}\)

\(151.\frac{a}{b}=\frac{1}{51}+\frac{1}{100}+\frac{1}{52}+\frac{1}{99}+......+\frac{1}{100}+\frac{1}{51}\)

\(\Rightarrow\left(151.\frac{a}{b}\right):2=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+.........+\frac{1}{100}\)

\(\Rightarrow\frac{a}{b}=\frac{2}{151}.\left(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+.........+\frac{1}{100}\right)\)

Chúc bn hok tốt

\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)

\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)

\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)

\(=4.\left(3+3^3+...+3^{2009}\right)\)

⇒ \(B\) ⋮ 4

b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)

1, \(\overline{a45b}\) \(⋮\) 2; 3; 5; 9 

⇒ b = 0; a + 4 + 5 + b ⋮ 9 ⇒ a + 9 ⋮ 9 ⇒ a = 9

Vậy \(\overline{a45b}\) = 9450

2, \(\overline{a1b8}\) \(⋮\) 2;3;9 ⇔ a + 1 + b + 8 ⋮ 9 ⇒ a + b ⋮ 9

⇒ b = 0; 1; 2; 3; 4; 5; 6; 7; 8

     a = 9; 8; 7; 6; 5; 4; 3; 2; 1

\(\Rightarrow\) \(\overline{a1b8}\) = 9108; 8118; 7128; 6138; 5148; 4158; 3168; 2178; 1188

3, 2025 + \(\overline{a36}\) \(⋮\)  3

  ⇔ 2 + 0 + 2 + 5 + a + 3 + 6 ⋮ 3

                    18 + a ⋮ 3 

                             a ⋮ 3 

 a = 0; 3; 6; 9 

4, 125 + 5¹⁰⁰ + \(\overline{31a}\) ⋮ 5

⇔ \(\overline{31a}\) ⋮ 5 

   a ⋮ 5 

   a = 0; 5

1) \(\overline{x45y}⋮2;3;5;9\)

\(\Rightarrow y=0\left(⋮2;5\right)\)

\(x+4+5+0⋮\left(3;9\right)\)

\(\Rightarrow x=9\)

\(\Rightarrow\overline{x45y}=9450\)

3) \(2025+\overline{x36}⋮3\)

mà \(2025⋮3\)

\(\Rightarrow\overline{x36}⋮3\)

\(\Rightarrow x+3+6⋮3\)

\(\Rightarrow x\in\left\{3;6;9\right\}\)

3) \(2022^{10}+4^{20}+\overline{53x}⋮2\)

\(2022^{10}=2022^8.2022^2=\overline{.....6}x\overline{....4}=\overline{.....4}⋮2\)

\(4^{20}=\overline{.....6}⋮2\)

\(\Rightarrow\overline{53x}⋮2\)

\(\Rightarrow x\in\left\{0;2;4;6;8\right\}\)

Sửa câu a

a)Ta có:

\(A=3+3^2+3^3+...+3^{99}\)

 \(A=\left(3+3^2+3^3\right)+...+\left(3^{97}+3^{98}+3^{99}\right)\) 

\(A=\left(3+3^2+3^3\right)+...+3^{96}.\left(3+3^2+3^3\right)\)

\(A=39+...+3^{96}.39\)

\(A=39.\left(1+...+3^{96}\right)\)

Vì 39 \(⋮\) 13 nên 39 . ( 1 + ... + 3⁹⁶ ) \(⋮\) 13

Vậy A \(⋮\) 13

_________

b)Ta có:

 \(B=5+5^2+5^3+...+5^{50}\)

\(B=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{49}+5^{50}\right)\)

\(B=\left(5+5^2\right)+5^2.\left(5+5^2\right)+...+5^{48}.\left(5+5^2\right)\)

\(B=30+5^2.30+...+5^{48}.30\)

\(B=30.\left(1+5^2+...+5^{48}\right)\)

Vì 30 \(⋮\) 6 nên 30. ( 1 + 5² + ... + 5⁴⁸ ) \(⋮\) 6

Vậy B \(⋮\) 6

a,A=3+3²+3³+..+3⁹⁹=(3+3²+3³)+...+(3⁹⁷+3⁹⁸+3⁹⁹)

     =3(1+3+3²)+...+3⁹⁷(1+3+3²)=3x13+...+3⁹⁷x13=13(3+...+97)⋮13

b,B=5+5²+...+5⁵⁰=(5+5²)+...+(5⁴⁹+5⁵⁰)=5(1+5)+..+5⁴⁹(1+5)

  =5x6+...+5⁴⁹x6=6(5+..+5⁴⁹)⋮6.