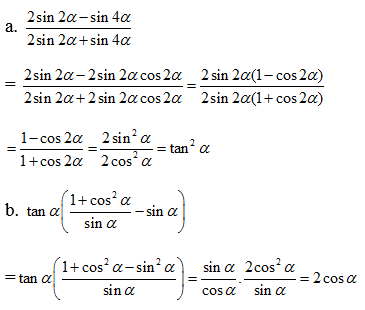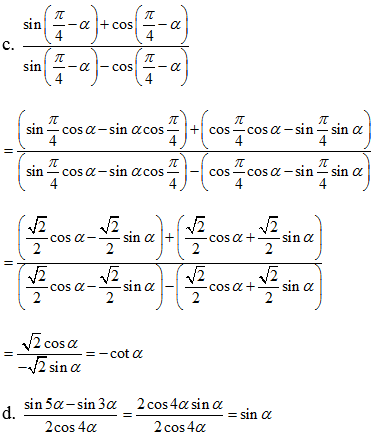\(\dfrac{sina+sin5a+sin3a}{cosa+cos5a+cos3a}=\dfrac{2sin3a.cos2a+sin3a}{2cos3a.cos2a+cos3a}=\dfrac{sin3a\left(2cos2a+1\right)}{cos3a\left(2cos2a+1\right)}=\dfrac{sin3a}{cos3a}=tan3a\)

\(\dfrac{1+sin4a-cos4a}{1+sin4a+cos4a}=\dfrac{1+2sin2a.cos2a-\left(1-2sin^22a\right)}{1+2sin2a.cos2a+2cos^22a-1}=\dfrac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\dfrac{sin2a}{cos2a}=tan2a\)

\(96\sqrt{3}sin\left(\dfrac{\pi}{48}\right)cos\left(\dfrac{\pi}{48}\right)cos\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)=48\sqrt{3}sin\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)\)

\(=24\sqrt{3}sin\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)=12\sqrt{3}sin\left(\dfrac{\pi}{6}\right)cos\left(\dfrac{\pi}{6}\right)\)

\(=6\sqrt{3}sin\left(\dfrac{\pi}{3}\right)=6\sqrt{3}.\dfrac{\sqrt{3}}{2}=9\)

\(A+B+C=\pi\Rightarrow A+B=\pi-C\Rightarrow tan\left(A+B\right)=tan\left(\pi-C\right)\)

\(\Rightarrow\dfrac{tanA+tanB}{1-tanA.tanB}=-tanC\Rightarrow tanA+tanB=-tanC+tanA.tanB.tanC\)

\(\Rightarrow tanA+tanB+tanC=tanA.tanB.tanC\)

Nhân cả tử và mẫu của phân số chứa tan với \(sina.cosa\)

\(A=\frac{sin^2x-cos^2x}{sin^2x+cos^2x}+cos2x=sin^2x-cos^2x+cos2x=-cos2x+cos2x=0\)

\(B=\frac{1+sin4a-cos4a}{1+sin4a+cos4a}=\frac{1+2sin2a.cos2a-\left(1-2sin^22a\right)}{1+2sin4a.cos4a+2cos^22a-1}\)

\(B=\frac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\frac{sin2a}{cos2a}=tan2a\)

\(C=\frac{3-4cos2a+2cos^22a-1}{3+4cos2a+2cos^22a-1}=\frac{2\left(cos^22a-2cos2a-1\right)}{2\left(cos^22a+2cos2a+1\right)}\)

\(C=\frac{\left(cos2a-1\right)^2}{\left(cos2a+1\right)^2}=\frac{\left(1-2sin^2a-1\right)^2}{\left(2cos^2a-1+1\right)^2}=\frac{sin^4a}{cos^4a}=tan^4a\)

\(D=\frac{sin^22a+4sin^4a-\left(2sina.cosa\right)^2}{4-4sin^2a-sin^22a}=\frac{sin^22a+4sin^4a-sin^22a}{4\left(1-sin^2a\right)-\left(2sina.cosa\right)^2}=\frac{4sin^4a}{4cos^2a-4sin^2a.cos^2a}\)

\(=\frac{sin^4a}{cos^2a\left(1-sin^2a\right)}=\frac{sin^4a}{cos^2a.cos^2a}=\frac{sin^4a}{cos^4a}=tan^4a\)

Mẫu số là \(-3cos2a\) hay \(-2cos2a\) vậy bạn? -3 không hợp lý

a) \(\dfrac{tan2\alpha}{tan4\alpha-tan2\alpha}=\dfrac{sin2\alpha}{cos2\alpha}:\left(\dfrac{sin4\alpha}{cos4\alpha}-\dfrac{sin2\alpha}{cos2\alpha}\right)\)
\(=\dfrac{sin2\alpha}{cos2\alpha}:\dfrac{sin4\alpha cos2\alpha-sin2\alpha cos4\alpha}{cos4\alpha cos2\alpha}\)
\(=\dfrac{sin2\alpha}{cos2\alpha}.\dfrac{cos4\alpha.cos2\alpha}{sin2\alpha}=cos4\alpha\).

b) \(\sqrt{1+sin\alpha}-\sqrt{1-sin\alpha}=\sqrt{sin^2\dfrac{\alpha}{2}+2sin\dfrac{\alpha}{2}cos\dfrac{\alpha}{2}+cos^2\dfrac{\alpha}{2}}\)\(-\sqrt{sin^2\dfrac{\alpha}{2}-2sin\dfrac{\alpha}{2}cos\dfrac{\alpha}{2}+cos^2\dfrac{\alpha}{2}}\)
\(=\sqrt{\left(sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right)^2}-\sqrt{\left(sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right)^2}\)
\(=\left|sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right|-\left|sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right|\)
Vì \(0< \alpha< \dfrac{\pi}{2}\) nên \(0< \alpha< \dfrac{\pi}{4}\).
Trong \(\left(0;\dfrac{\pi}{4}\right)\) thì \(sin\dfrac{\alpha}{2}\) tăng dần từ 0 tới \(\dfrac{\sqrt{2}}{2}\) và \(cos\dfrac{\alpha}{2}\) giảm dần từ 1 tới \(\dfrac{\sqrt{2}}{2}\) nên \(\left|sin\dfrac{\alpha}{4}-cos\dfrac{\alpha}{4}\right|=-\left(sin\dfrac{\alpha}{4}-cos\dfrac{\alpha}{4}\right)=cos\dfrac{\alpha}{4}-sin\dfrac{\alpha}{4}\).
Vì vậy:
\(\left|sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right|-\left|sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right|\)
\(=sin\dfrac{\alpha}{4}+cos\dfrac{\alpha}{4}-\left(cos\dfrac{\alpha}{4}-sin\dfrac{\alpha}{4}\right)=2sin\dfrac{\alpha}{4}\).

c) \(\dfrac{3-4cos2\alpha+cos4\alpha}{3+4cos2\alpha+cos4\alpha}\)\(=\dfrac{4-4cos2\alpha+cos4\alpha-1}{4+4cos2\alpha+cos4\alpha-1}\)
\(=\dfrac{4\left(1-cos2\alpha\right)-2sin^22\alpha}{4\left(1+cos2\alpha\right)-2sin^22\alpha}\)
\(=\dfrac{4cos^2\alpha-2sin^22\alpha}{4sin^2\alpha-2sin^22\alpha}\)
\(=\dfrac{4cos^2\alpha-8sin^2\alpha cos^2\alpha}{4sin^2\alpha-8sin^2\alpha cos^2\alpha}\)
\(=\dfrac{4cos^2\alpha\left(1-2sin^2\alpha\right)}{4sin^2\alpha\left(1-2cos^2\alpha\right)}=cot^2\alpha.\dfrac{cos2\alpha}{-cot2\alpha}\)
\(=-cot^2\alpha\).