Cho x , y là nghiệm của hệ
x + y = m
x2 + y2 = -m2 + 6
Tìm Min , Max của F = xy - 6(x + y)
Biết cặp số (x; y) là nghiệm của hệ x + y = m x 2 + y 2 = - m 2 + 6 . Tìm giá trị của m để P = xy + 2(x + y) đạt giá trị nhỏ nhất.
A. m = −1
B. m = −2
C. m = 1
D. m = 0
cho x, y là nghiệm của hệ \(\left\{{}\begin{matrix}x+y=m+1\\xy=m^2-2m+2\end{matrix}\right.\). tìm min, max của F=\(x^2+y^2\)
Theo Viet đảo, x và y là nghiệm của pt:
\(t^2-\left(m+1\right)t+m^2-2m+2=0\)
Để hệ đã cho có nghiệm \(\Leftrightarrow\Delta\ge0\)
\(\Rightarrow-3m^2+10m-7\ge0\Rightarrow1\le m\le\frac{7}{3}\)
Khi đó ta có: \(F=x^2+y^2=\left(x+y\right)^2-2xy\)
\(F=\left(m+1\right)^2-2\left(m^2-2m+2\right)\)
\(=-m^2+6m-3\)
Xét hàm \(f\left(m\right)=-m^2+6m-3\) trên \(\left[1;\frac{7}{3}\right]\)
\(-\frac{b}{2a}=3\notin\left[1;\frac{7}{3}\right]\) ; \(f\left(1\right)=2\) ; \(f\left(\frac{7}{3}\right)=\frac{50}{9}\)
\(\Rightarrow F_{max}=\frac{50}{9}\) khi \(m=\frac{7}{3}\)
\(F_{min}=2\) khi \(m=1\)
Tìm min, max của P = x2 + y2 với x, y là các số thực không âm và x + y + xy = 15
\(\left(x^2+9\right)+\left(y^2+9\right)+3\left(x^2+y^2\right)\ge6x+6y+6xy=90\)
\(\Rightarrow4\left(x^2+y^2\right)+18\ge90\)
\(\Rightarrow x^2+y^2\ge18\)
\(P_{min}=18\) khi \(x=y=3\)
\(x+y+xy=15\Rightarrow\left\{{}\begin{matrix}x\le15\\y\le15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\left(x-15\right)\le0\\y\left(y-15\right)\le0\end{matrix}\right.\)
\(\Rightarrow x^2+y^2\le15x+15y\) (1)
Cũng từ đó ta có: \(\left(x-15\right)\left(y-15\right)\ge0\Rightarrow xy\ge15x+15y-225\)
\(\Rightarrow16x+16y-225\le x+y+xy=15\)
\(\Rightarrow x+y\le15\) (2)
(1);(2) \(\Rightarrow x^2+y^2\le15.15=225\)
\(P_{max}=225\) khi \(\left(x;y\right)=\left(0;15\right);\left(15;0\right)\)
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình x y + y 2 + x = 7 y ( 1 ) x 2 y + x = 12 ( 2 ) thì tích xy bằng:
A. 1
B. 2
C. 3
D. 4
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

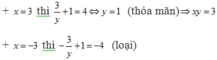

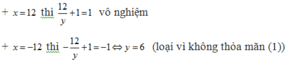
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
Tập nghiệm của hệ phương trình x + y + x y = - 13 x 2 + y 2 - x - y = 32 là:
A. - 5 ; 2 ; 5 ; - 3
B. - 5 ; 2 ; 5 ; - 3 ; - 3 ; 5
C. - 5 ; 2 ; - 2 ; 5 ; 5 ; - 3 ; - 3 ; 5
D. - 5 ; 2 ; 2 ; - 5 ; 5 ; - 3 ; - 3 ; 5
t 2
Ta có: x + y + x y = - 13 x 2 + y 2 - x - y = 32 ⇔ x + y + x y = - 13 ( x + y ) 2 - 2 x y - ( x + y ) = 32
Đặt S = x+ y; P = xy . Khi đó, hệ phương trình trên trở thành:
S + P = - 13 ( 1 ) S 2 - 2 P - S = 32 ( 2 )
Từ (1) suy ra: P = -S – 13 thay vào (2) ta được:
S 2 – 2(-S – 13) – S = 32
⇔ S 2 + 2 S + 26 - S - 32 = 0 ⇔ S 2 + S - 6 = 0 ⇔ [ S = 2 S = - 3
* Với S = 2 thì P = -15 . Khi đó , x và y là nghiệm phương trình:
t 2 - 2t – 15 = 0 ⇔ [ t = 5 t = - 3
* Với S = -3 thì P = -10. Khi đó, x và y là nghiệm phương trình:
t 2 + 3t – 10 =0 ⇔ [ t = 2 t = - 5
Vậy hệ phương trình đã cho có 4 nghiệm ( 5; -3); (-3; 5); (2; -5); (-5; 2).
Chọn D.
Cho x,y là 2 số thực không âm thay đổi.
Tìm min và max của `P=((x-y)(1-xy))/((1+x)^2(1+y)^2)`
Ta có: \(\left(x-y\right)\left(1-xy\right)\le\dfrac{1}{4}\left(x-y+1-xy\right)^2=\dfrac{1}{4}\left(x+1\right)^2\left(1-y\right)^2\)
\(\Rightarrow P\le\dfrac{\left(1+x\right)^2\left(1-y\right)^2}{4\left(1+x\right)^2\left(1+y\right)^2}=\dfrac{1}{4}\left(\dfrac{y^2-2y+1}{y^2+2y+1}\right)=\dfrac{1}{4}\left(1-\dfrac{4y}{y^2+2y+1}\right)\le\dfrac{1}{4}\)
\(P_{max}=\dfrac{1}{4}\) khi \(\left(x;y\right)=\left(1;0\right)\)
Lại có:
\(\left(y-x\right)\left(1-xy\right)\le\dfrac{1}{4}\left(y-x+1-xy\right)^2=\dfrac{1}{4}\left(1+y\right)^2\left(1-x\right)^2\)
\(\Rightarrow-P\le\dfrac{\left(1+y\right)^2\left(1-x\right)^2}{4\left(1+y\right)^2\left(1+x\right)^2}=\dfrac{1}{4}\left(\dfrac{1-2x+x^2}{1+2x+x^2}\right)=\dfrac{1}{4}\left(1-\dfrac{4x}{x^2+2x+1}\right)\le\dfrac{1}{4}\)
\(\Rightarrow-P\le\dfrac{1}{4}\Rightarrow P\ge-\dfrac{1}{4}\)
\(P_{min}=-\dfrac{1}{4}\) khi \(\left(x;y\right)=\left(0;1\right)\)
(Do \(y\ge0\Rightarrow\dfrac{4y}{y^2+2y+1}\ge0\Rightarrow1-\dfrac{4y}{y^2+2y+1}\le1\Rightarrow...\))
Cho hệ phương trình: 2 x 2 + x y − y 2 = 0 x 2 − x y − y 2 + 3 x + 7 y + 3 = 0 . Các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là:
A. (2; −2), (3; −3).
B. (−2; 2), (−3; 3).
C. (1; −1), (3; −3).
D. (−1; 1), (−4; 4).
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
Biết cặp số (x; y) là nghiệm của hệ x + y = 2 m x 2 + y 2 = 2 m + 2 . Tìm giá trị của m để P = xy – 3 (x + y) đạt giá trị nhỏ nhất.
A. m = - 7 2
B. m = −7
C. m = 7
D. m = 7 2
Cho hệ: x+y+z=3 và xy+yz+xz=-9
Tìm Min, Max của xyz