Giải dùm câu 54 ạ

Những câu hỏi liên quan
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
các bạn giải dùm mìh câu này vs ạ
tìm số có 2 chữ số biết rằg tổg hai chữ số của nó bằng 10 và số đos lơsn hơn số viết thheo thứ tự ngược lại là 54 đown vị
giải dùm mình câu nào cũng dc ạ 😞 3 câu luôn càng tốt ạ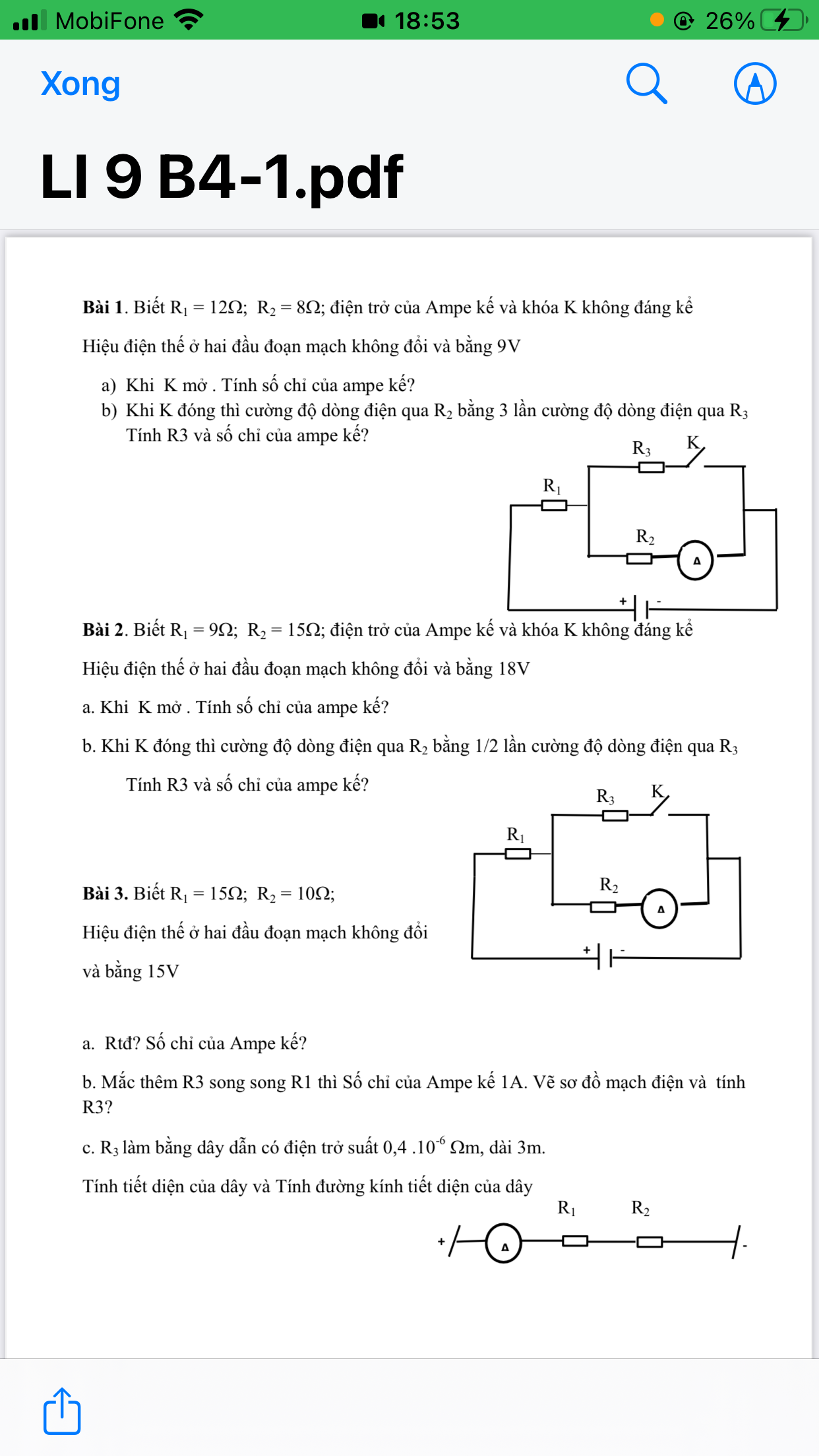
Giải dùm em câu 2 với câu 3 đi ạ
2)
Đổi 1h15 phút thành 1,25 h
Thời gian dự định là: $\frac{AB}{40}$ (h)
Thời gian thực tế: $\frac{AB}{40-15}=\frac{AB}{25}$ (h)
Chênh lệch thời gian dự định và thời gian thực tế là:
$\frac{AB}{25}-\frac{AB}{40}=1,25$
$\frac{3AB}{200}=1,25\Rightarrow AB=83,33$ (km)
Đúng 0
Bình luận (0)
Câu 3:
Đổi 20 phút thành $\frac{1}{3}$ giờ
Giả sử sau khi ô tô đi được $a$ giờ thì hai xe gặp nhau tại $C$. Lúc này, xe máy đã đi được $a+\frac{1}{3}$ giờ
Ta có:
$AC=35(a+\frac{1}{3})=(35+20).a$
$\Leftrightarrow 35(a+\frac{1}{3})=55a$
$\Rightarrow a=\frac{7}{12}$ (h)
Đổi $\frac{7}{12}$ h = 35 phút. Vậy sau khi đi được 35 phút thì ô tô gặp xe máy.
Đúng 0
Bình luận (0)
Giải dùm mình câu h ạ
1.\(x^2+4x+4=\left(x+2\right)^2\)
2.\(x^2-8x+16=\left(x-4\right)^2\)
3.\(\left(x+5\right)\left(x-5\right)=x^2-25\)
4.\(x^3+12x+48x+64=\left(x+4\right)^3\)
5.\(x^3-6x^2+12x-8=\left(x-2\right)^3\)
6.\(\left(x+2\right)\left(x^2-2x+4\right)=x^3+8\)
7.\(\left(x-3\right)\left(x^2+3x+9\right)=x^3-27\)
8.\(4x^4-15=\left(2x^2\right)^2-\left(\sqrt{15}\right)^2=\left(2x^2-\sqrt{15}\right)\left(2x^2+\sqrt{15}\right)\)
Đúng 0
Bình luận (0)
Giải dùm em câu 8 ạ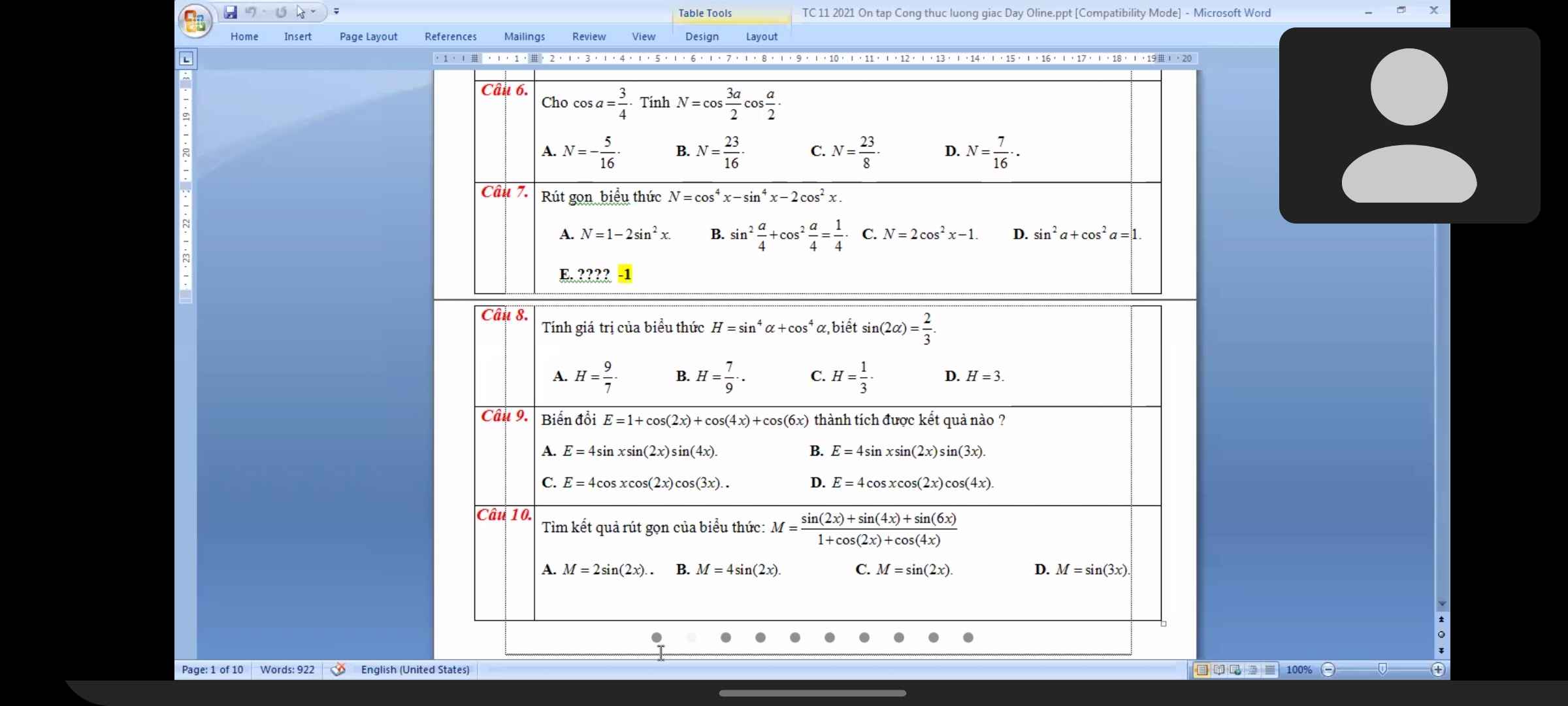
Lời giải:
$H=(\sin ^2a+\cos ^2a)^2-2\sin ^2a\cos ^2a$
$=1-\frac{1}{2}(2\sin a\cos a)^2=1-\frac{1}{2}(\sin 2a)^2=1-\frac{2}{9}=\frac{7}{9}$
Đáp án B.
Đúng 1
Bình luận (0)
Giải và vẽ trục dùm em với please 😭😭 (giải chi tiết dùm em câu này nhé,em ko hiểu cách tính của câu như vậy í ạ 😢😭)
\(\dfrac{2x+2}{3}< 2+\dfrac{x-2}{2} \Leftrightarrow2\left(2x+2\right)< 12+3\left(x-2\right) \Leftrightarrow4x+4< 3x+6 \Leftrightarrow4x< 3x+2 \Leftrightarrow x< 2\)
Đúng 0
Bình luận (0)
Giải dùm câu ba với ạ, đang cần gấp, cảm ơn ạ
Giải dùm mình câu này với ạ
Đọc tiếp
Giải dùm mình câu này với ạ
`(1+2cosx)(3-cosx)=0`
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cosx=3\left(L\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{-2\pi}{3}+k2\pi\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{2\pi}{3}+k\pi\)
`(k \in ZZ)`
Đúng 3
Bình luận (0)
\(\Leftrightarrow\left[{}\begin{matrix}1+2\cos x=0\\3-\cos x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=-\dfrac{1}{2}\\\cos x=3\end{matrix}\right.\)
Mà \(-1\le\cos x\le1\)
\(\Rightarrow\cos x=-\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{4}{3}\pi+k2\pi\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Giải dùm em câu này với ạ
Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{0}\Leftrightarrow\overrightarrow{A'G}+\overrightarrow{GA}+\overrightarrow{B'G}+\overrightarrow{GB}+\overrightarrow{C'G}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Goi G la trong tam tam giac A'B'C'
Lai co: \(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{0}\)
\(\Rightarrow G'\equiv G\Rightarrow G'=\left(1;0;-2\right)\)
Đúng 2
Bình luận (0)






















