1. Có ba hộp đựng cầu. Hộp 1 đựng 10 cầu trắng và 5 cầu đỏ, hộp 2 đựng 7 cầu trắng và 8 cầu đỏ, hộp 3 đựng 5 cầu trắng. Lấy ngẫu nhiên từ hộp 1 ra 2 quả cầu và từ hộp 2 ra 1 quả cầu rồi bỏ vào hộp 3. Tính xác suất để hộp thứ 3 toàn cầu trắng.

Những câu hỏi liên quan
Có 3 hộp đựng cầu. Hộp 1 đựng 5 cầu đen, 10 cầu trắng, hộp 2 đựng 8 cầu đen, 7 cầu trắng, hộp 3 đựng 1 cầu đen, 2 cầu trắng. Lấy ngẫu nhiên từ hộp 1 ra 2 quả cầu và từ hộp 2 ra 1 quả cầu bỏ vào hộp thứ 3 rồi từ hộp 3 lấy ngẫu nhiên ra 1 quả cầu. Tính xác suất lấy được cầu đen.
1. Có hai hộp đựng cầu. Hộp 1 có 5 cầu đen và 10 cầu trắng; hộp 2 có 8 cầu đen và 15 cầu trắng. Lấy ngẫu nhiên 1 quả cầu từ hộp 1 bỏ sang hộp 2, sau đó từ hộp 2 lấy ngẫu nhiên ra 1 quả cầu. Tính xác suất để lấy được cầu trắng.
Một hộp đựng 7 quả cầu trắng và 3 quả cầu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu được lấy có đúng 2 quả cầu đỏ. A.
20
71
.
B.
21
71
.
C.
21
70
.
D.
62
211
.
Đọc tiếp
Một hộp đựng 7 quả cầu trắng và 3 quả cầu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu được lấy có đúng 2 quả cầu đỏ.
A. 20 71 .
B. 21 71 .
C. 21 70 .
D. 62 211 .
Một hộp đựng 7 quả cầu trắng và 3 quả cầu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu được lấy có đúng 2 quả cầu đỏ.
Đọc tiếp
Một hộp đựng 7 quả cầu trắng và 3 quả cầu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu được lấy có đúng 2 quả cầu đỏ.
![]()
![]()
![]()
![]()
Đáp án C.
Số cách lấy ngẫu nhiên 4 quả là: C 10 4 (cách)
Số cách lấy được 2 quả đỏ, 2 trắng là: C 4 2 . C 7 2 (cách)
Xác suất để lấy được đúng 2 quả đỏ là:
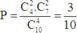
Đúng 0
Bình luận (0)
Đáp án C.
Số cách lấy được 2 quả đỏ, 2 trắng là: C 4 2 . C 7 2 (cách)
Xác suất để lấy được đúng 2 quả đỏ là:
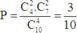
Đúng 0
Bình luận (0)
Một hộp đựng 7 quả cầu màu trắng và 3 quả cầu màu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu đỏ
A. 21/71
B. 20/71
C. 62/211
D. 21/70
1. Có 3 hộp đựng cầu. Hộp 1 đựng 5 cầu đen, 10 cầu trắng, hộp 2 đựng 8 cầu đen, 7 cầu trắng, hộp 3 đựng 1 cầu đen, 2 cầu trắng. Lấy ngẫu nhiên từ hộp 1 ra 2 quả cầu và từ hộp 2 ra 1 quả cầu bỏ vào hộp thứ 3 rồi từ hộp 3 lấy ngẫu nhiên ra 1 quả cầu. Tính xác suất lấy được cầu đen.
Đọc tiếp
1. Có 3 hộp đựng cầu. Hộp 1 đựng 5 cầu đen, 10 cầu trắng, hộp 2 đựng 8 cầu đen, 7 cầu trắng, hộp 3 đựng 1 cầu đen, 2 cầu trắng. Lấy ngẫu nhiên từ hộp 1 ra 2 quả cầu và từ hộp 2 ra 1 quả cầu bỏ vào hộp thứ 3 rồi từ hộp 3 lấy ngẫu nhiên ra 1 quả cầu. Tính xác suất lấy được cầu đen.
Hai hộp chứa các quả cầu. Hộp I đựng 3 quả cầu đỏ và 2 quả cầu xanh, hộp II đựng 4 quả cầu đỏ và 6 quả cầu xanh. Lấy ngẫu nhiên từ mỗi hộp 1 quả. Kí hiệu: A: “Quả lấy từ hộp I màu đỏ”. B: “Quả lấy từ hộp II màu đỏ”. a) Xét xem A, B có độc lập không? b) Tính xác suất dựa trên A, B sao cho: + Hai quả lấy ra đều màu đỏ. + Hai quả lấy ra cùng màu. + Hai quả lấy ra khác màu.
Đọc tiếp
Hai hộp chứa các quả cầu. Hộp I đựng 3 quả cầu đỏ và 2 quả cầu xanh, hộp II đựng 4 quả cầu đỏ và 6 quả cầu xanh. Lấy ngẫu nhiên từ mỗi hộp 1 quả. Kí hiệu: A: “Quả lấy từ hộp I màu đỏ”. B: “Quả lấy từ hộp II màu đỏ”. a) Xét xem A, B có độc lập không? b) Tính xác suất dựa trên A, B sao cho: + Hai quả lấy ra đều màu đỏ. + Hai quả lấy ra cùng màu. + Hai quả lấy ra khác màu.
a) Vì số bi trong hộp thứ nhất và hộp thứ hai là độc lập và việc lấy ra số các bi từ hai hộp là độc lập nên hai biến cố A, B là độc lập.
b)
- Trên A:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_3}{C^2_5}=\frac{3}{10}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_3+C^2_2}{C^2_5}=\frac{4}{10}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{4}{10}=\frac{6}{10}\).
- Trên B:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_4}{C^2_{10}}=\frac{2}{15}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_4+C^2_6}{C^2_{10}}=\frac{7}{15}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{7}{15}=\frac{8}{15}\).
Từ một hộp chứa 5 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để lấy được 2 quả không trắng. A. B. C. D.
Đọc tiếp
Từ một hộp chứa 5 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để lấy được 2 quả không trắng.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
Gọi ![]() là không gian mẫu.
là không gian mẫu.
Ta có ![]()
Gọi D là biến cố: lấy được 2 quả cầu không trắng.
Ta có
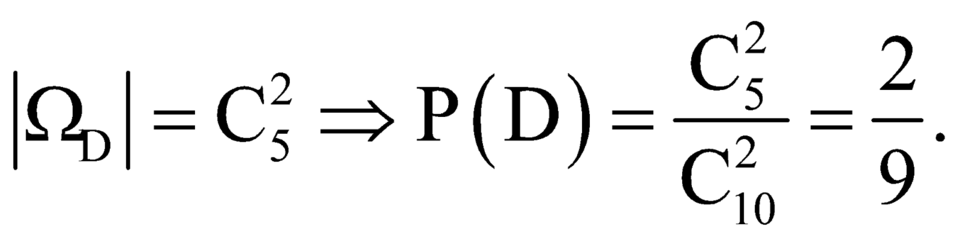
Đúng 0
Bình luận (0)
Từ một hộp chứa 5 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để lấy được 2 quả không trắng. A.
2
9
B.
16
45
C.
1
15
D.
10
29
Đọc tiếp
Từ một hộp chứa 5 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để lấy được 2 quả không trắng.
A. 2 9
B. 16 45
C. 1 15
D. 10 29









