b) Cho tam giác ABC có 3 góc nhọn. Gọi O là trung điểm của BC. Gọi D là điểm đối xứng của A qua BC ; DE là điểm đối xứng của A qua O.Chứng minh rằng BCED là hthang cân.

Những câu hỏi liên quan
Cho ∆ABC có 3 góc nhọn. Gọi O là trung điểm của BC. Gọi D là điểm đối xứng của A qua BC, E là điểm đối xứng của A qua O. Cm BCED là hình thang cân.
Cho tam giác ABC có ba góc nhọn. Gọi O là trung điểm của BC. Gọi D là điểm đối xứng của A qua BC; E là điểm đối xứng của A qua O.
Đề yêu cầu CMR : BCED là hình thang cân ??
Ta có : A đối xứng D qua BC , gọi AD cắt BC tại H ta có AD \(\perp\) BC tại H và AH = HD
Xét tg ADE ta có ; AH = HD , AO = OE
=> OH // DE hay BC // DE .
tứ giác BCED có BC//DE => BCED là hih thang .
Xét tg OAB và tg OEC có :
OB = OC , OA = OE , góc AOB = góc COE
=> tg OAB = tg OEC => góc ABO = góc OCE (1).
Có : BH \(\perp\) AD tại trung điểm H của AD
=> BAD cân tại B => góc ABH = góc HBD (2) .
Từ (1) và (2) có : góc HBD = góc OCE
=> hih thang BCED có : góc HBD = góc OCE
=> BCED là hih thang cân .
Xem thêm tại : Câu hỏi của Quang Trần - Toán lớp 8 | Học trực tuyến ( https://h.vn/hoi-dap/question/674960.html )
Gợi ý cho bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có 3 góc nhọn(AB<AC). Gọi H là trực tâm, O là giao điểm của 3 đường trung trực của tam giác. Gọi D là điểm đối xứng của điểm A qua O.
a)Chứng minh rằng tứ giác BHCD là hình bình hành
b)Gọi M là trung điểm của BC, chứng minh AH=2MO
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:
b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
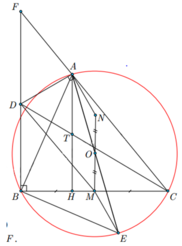
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
Đúng 0
Bình luận (0)
bài 1 Cho tam giác nhọn ABC có AB<AC , đương cao D và CE cắt nhau tại H. I là trung BC . Gọi K là đối xứng của H qua I , M là điểm đối xứng qua BC
a, Cm BHCk là hình bình hành
b, gọi o là trung điểm DK . chứng minh O là giao điểm của 3 đường trung trực của tam giác ABC
c, Cm AK vuông góc DE
Giúp mình với tối mai đi hc rồi
câu a thì dễ mà caaub vẽ thế nào cx ko là giao ba đường đấy
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AB< AC, các đường cao BD và CE cắt nhau tại H, I là trung điểm của BC. Gọi K là điểm đối xứng với H qua I, M là điểm đối xứng với H qua đường thẳng BC.
a, Các tứ giác BHCK,BCKM là hình gì?
b, Gọi O là trung điểm của AK. Chứng minh O là giao điểm cảu ba đường trung trưc của tam giác ABC
c, Chứng minh rằng AK vuông góc với DE
ho tam giác BEC có 3 góc nhọn ( EB < BC ). Dường cao BA . Gọi I ; N lần lượt là trung điểm của Bc và AC .
a) Gọi M là điểm đối xứng của A qua I . C/m ABMC là hình chữ nhật
b) Gọi D là điểm đối xứng của I qua AC. Tứ giác ADCI là hình j? Ví sao ?
c) Vẽ AH vuông góc vs BC. C/m HA . AM = MC . CA
d) Đường thẳng BN cắt DC tại K. C/m diện tích ADC = 3 diện tích ADK
bạn vẽ hình rồi chụp cho mình giải cho
Đúng 0
Bình luận (1)
a) Ta có: M là điểm đối xứng của A qua I
=> I là trung điểm của MA(t/c)
I là trung điểm của BC(gt)
Xét tứ giác ABMC có:
2 đường chéo cắt nhau tại trung điểm mỗi đường
=> tứ giác ABMC là hình chữ nhật(dhnb)
Đúng 0
Bình luận (0)
câu b là sao v? xem lại giúp mk cái đề với
Đúng 0
Bình luận (0)
1. cho tam giác ABC , gọi m là đường trung trực của BC . Vẽ điểm D đối xứng với A qua m .a, tìm các đoạn thẳng đối xứng với AB , AC qua mb, Xác định dạng tứ giác ABCD2. Cho tam giác ABC . Trên đường thẳng d lấy điểm M ≠≠A . C/m : AB + AV BM+MC3. Cho tam giác nhọn ABC , M thuộc cạnh BC , gọi D là điểm đối xứng với M qua AB , gọi E là điểm đối xứng với M qua AC , gọi I , K là giao điểm của DE với AB , AC . c/m : MA là tia phân giác của góc IMK help me
Đọc tiếp
1. cho tam giác ABC , gọi m là đường trung trực của BC . Vẽ điểm D đối xứng với A qua m .
a, tìm các đoạn thẳng đối xứng với AB , AC qua m
b, Xác định dạng tứ giác ABCD
2. Cho tam giác ABC . Trên đường thẳng d lấy điểm M ≠≠A . C/m : AB + AV < BM+MC
3. Cho tam giác nhọn ABC , M thuộc cạnh BC , gọi D là điểm đối xứng với M qua AB , gọi E là điểm đối xứng với M qua AC , gọi I , K là giao điểm của DE với AB , AC . c/m : MA là tia phân giác của góc IMK
help me
Bài 2 : c/m là AB+AC<BM+MC nha mấy bạn giúp mk vs
Đúng 0
Bình luận (0)
Cho tam giác abc có ba góc nhọn biết AB nhỏ hơn AC Gọi M N lần lượt là trung điểm của AB AC a)Chứng minh tứ giác mncb là hình thang b) Gọi D là trung điểm của BC Chứng minh tứ giác MNCD là hình bình hành c) Gọi E là điểm đối xứng của d qua n Chứng minh tứ giác ADCE là hình bình hành d) tam giác ABC cần thêm điều kiện gì để tam giác tứ giác ABCE thành hình chữ nhật
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MNCB là hình thang
b: Xét tứ giác MNCD có
MN//CD
MN=CD
Do đó: MNCD là hình bình hành
c: Xét tứ giác ADCE có
N là trung điểm của AC
N là trung điểm của DE
Do đó:ADCE là hình bình hành
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn có AB <AC, các đường cao BD và CE cắt nhau tại H, I là trung điểm BC. gọi K là điểm đối xứng với H qua I, M là điểm đối xứng với H qua AB.
a) các tứ giác BHCK , BCKM là hình gì? vì sao?
b) gọi o là tđ của AK.
CM : o là giao điểm của 3 đường trung trực của tam giác ABC
c) CM : AK vuông góc DE
Hiểu rõ về BTS chỉ có thể là Army phải không chị Bangtan?Chỉ cần nhìn avatar đoán ra chủ nick là con gái vì số fan girl nhiều hơn fan boy.





















