Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục củng thẳng hàng. Chứng minh câu nói đó là đúng

Những câu hỏi liên quan
Các câu sau đúng hay sai?
a) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng đường thẳng hàng.
b) Hai tam giác đối xứng với nhau qua một truc thì có chu vi bằng nhau.
c) Một đường tròn có vô số trục đối xứng.
d) Một đoạn thẳng chỉ có một trục đối xứng.
b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.
c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.
d) Sai.
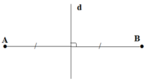
Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.
Đúng 0
Bình luận (0)
Các câu sau đúng hay sai ?
a) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng thẳng hàng
b) Hai tam giác đối xứng với nhau qua một trục thì có chu vi bằng nhau
c) Một đường tròn có vô số trục đối xứng
d) Một đoạn thẳng chỉ có một trục đối xứng
a) đúng
b) đúng
c) đúng
d) sai
Giải thích: Đoạn thẳng AB trên hình bên có hai trục đối xứng đó là đường thẳng AB và đường trung trực của đoạn AB.
Đúng 0
Bình luận (2)
Các câu sau đây câu nào đúng câu nào sai?
A) một đường tròn có một số trục đối xứng
B) một đoạn thẳng chỉ có một trục đối xứng
C) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng quanh một trục cũng thẳng hàng
D) hai hình tam giác đối xứng với nhau qua một trục thì có chu vi bằng nhau
AG:NAM LẦY BÁNH FREE FREE RẤT NGỎI
chứng minh rằng nếu ba điểm A,B và C không thẳng hàng thì các điểm A', B' và C' đối xứng với chúng qua điểm O cũng không thẳng hàng
A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của ΔABC
=>\(AB+AC>BC;AC+BC>AB;BC+AC>AB\)
Xét tứ giác ABA'B' có
O là trung điểm chung của A'A và BB'
nên ABA'B' là hình bình hành
=>AB=A'B'
Xét tứ giác AC'A'C có
O là trung điểm chung của A'A và C'C
nên AC'A'C là hình bình hành
=>AC=A'C'
Xét tứ giác BC'B'C có
O là trung điểm chung của BB' và CC'
nên BC'B'C là hình bình hành
=>BC=B'C'
\(AB+AC>BC\)
mà AB=A'B' và AC=A'C' và BC=B'C'
nên \(A'B'+A'C'>B'C'\left(1\right)\)
AC+BC>AB
mà AC=A'C' và BC=B'C' và AB=A'B'
nên A'C'+B'C'>A'B'(2)
BA+BC>AC
mà BA=B'A' và BC=B'C' và AC=A'C'
nên B'A'+B'C'>A'C'(3)
Từ (1),(2),(3) suy ra A'B'A'C'B'C' là ba cạnh của một tam giác
=>A',B',C' không thẳng hàng(ĐPCM)
Đúng 0
Bình luận (0)
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu
A
B
→
p
A
C
→
t
h
ì
A
B
→
p...
Đọc tiếp
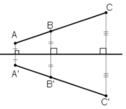
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu A B → = p A C → t h ì A ' B ' → = p A ' C ' → , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
Để ý rằng
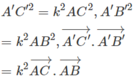
Ta có:
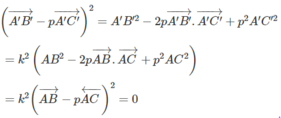
Từ đó suy ra 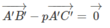
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Đúng 0
Bình luận (0)
Câu 27. Xét các khẳng định sau:
(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.
(II) Qua hai điểm ta vẽ được một đường tròn.
(III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
(IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn.
Số khẳng định đúng là
Câu 27. Xét các khẳng định sau:(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.(II) Qua hai điểm ta vẽ được một đường tròn. (III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn. (IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn. Số khẳng định đúng là A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Câu 27. Xét các khẳng định sau:
(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.
(II) Qua hai điểm ta vẽ được một đường tròn.
(III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
(IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn.
Số khẳng định đúng là
A. 1 B. 2 C. 3 D. 4
gọi D là điểm đối xứng với M qua AB , E là điểm đôí xứng với M qua AC
a, chứng minh ba điểm D, A, E thẳng hàng
b, chứng minh BC //CE
c, điểm M ở vị trí nào trên BC thì đoạn DE có độ dài nhỏ nhất
Gọi A, B và C tương ứng là ảnh của ba điểm A, B,C qua phép đồng dạng. Chứng minh rằng nếu overrightarrow{AB}poverrightarrow{AC} thì overrightarrow{AB}poverrightarrow{AC} trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng nếu điểm B nằm giữa hai điểm A và C thì điểm B nằm giữa hai điểm A và C ?
Đọc tiếp
Gọi A', B' và C' tương ứng là ảnh của ba điểm A, B,C qua phép đồng dạng. Chứng minh rằng nếu \(\overrightarrow{AB}=p\overrightarrow{AC}\) thì \(\overrightarrow{A'B'}=p\overrightarrow{A'C}'\) trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A' và C' ?





















