100 E B C A D 120 140 Hãy chứng tỏ AB song song CD
Đọc tiếp
Hãy chứng tỏ AB song song CD
Những câu hỏi liên quan
cho hình vẽ . chứng minh AB song song với CD B A E C D 100 độ 120 độ 140 độ
cho hình thang biết : A = C = 100 độ; D = 80 độ
Chứng tỏ ; a, AB song song CD
b. AD song song BC
Cho Om là phân giác xOy, On là tia đối Om, biết nOx = 100 độ
a, Chúng tỏ AB song song CD
b. Chứng tỏ BC song song CD
Hình hang ABCD có AB song song với CD.Tia phân giác trong của góc A và góc B cắt nhau ở E. E thuộc CD
Chứng tỏ CD=AD+BC
Vì AB//CD =>góc BAE=góc AED(so le trong);ABE=BEC(so le trong)
Mà DAE=EAB(gt);ABE=EBC(gt)=>DAE=AED;EBC=BEC
=>tam giác ADE cân tại D;tam giác BEC cân tại C
=>AD=DE;BC=EC =>AD+BC=DE+EC
=>AD+BC=CD(ĐPCM)
Đúng 0
Bình luận (0)
Cho góc xAB =40° ABy'=140° DCy=130°
Chứng tỏ Ax song song với yy'
Chứng minh CD vuông góc với AB
Cho tam giác ABC, tia phân giác của góc C cắt AB tại D, qua A kẻ đườn thẳng song song Cd cắt đường thẳng BC tại E. Chứng tỏ rằng góc cae = góc CEA
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
Đúng 0
Bình luận (0)
chứng tỏ AB//EF trong mỗi hình sauhình a A B C D E F 120 độ 60 độ 40 độ 140 độ hình b C D E F A B 30 độ 30 độ 40 độ 40 độ
Đọc tiếp
chứng tỏ AB//EF trong mỗi hình sau
hình a
hình b
hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
Đúng 2
Bình luận (0)
Trên cung nhỏ
A
B
⏜
của (O), cho hai điểm C và D sao cho cung
A
B
⏜
được chia thành ba cung bằng nhau (
A
C
⏜
C
D
⏜
D...
Đọc tiếp
Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song
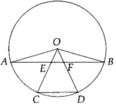
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
Đúng 0
Bình luận (0)
Cho hai tam giác ABC, ABD vuông ở C và D (C,D khác phía A,B). Lấy M là trung điểm AB.
a) Tam giác MCD là tam giác gì?
b) Lấy H là trung điểm của CD, kẻ AK vuông góc vs CD ( K thuộc CD). Chứng minh: MH song song AK
c) Biết MH cắt BK ở E. Kẻ EN song song CD (N thuộc BC). Chứng minh: NB=NC
Cho tám giác ABC có M là trung điểm của BC. Trên tia đối AM lấy điểm D sao cho M là trung điểm của AD: a) Chứng Minh tam giác ABM= tam giác DCM. b) Chứng minh AB song song CD. c) Qua C kẻ đường thẳng song song với AD cắt AB kéo dài tại E. Chứng minh A là trung điểm của BE
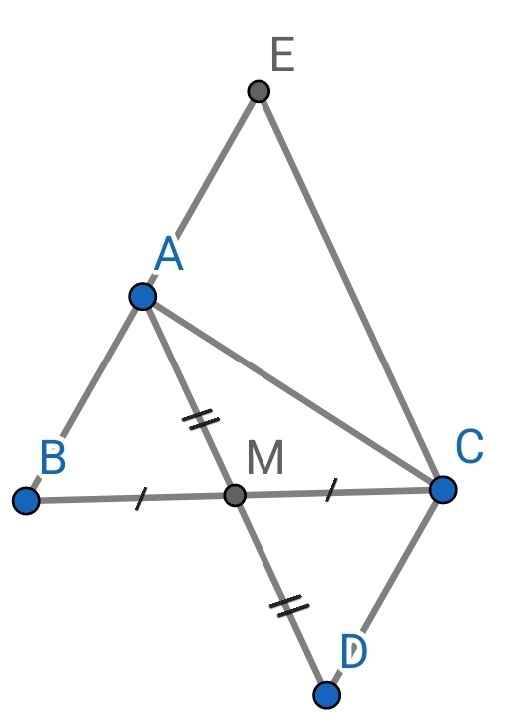a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
Đúng 0
Bình luận (0)