Bạn xem đã viết đúng đề chưa vậy?

a) P(x)=4x²-6x+a; Q(x)=x-3

Lấy P(x):Q(x)=4x-6 dư a+30

Vậy để P(x)⋮Q(x) ⇒ a+30=0 ⇒ a=-30

b) P(x)=2x²+x+a; Q(x)=x+3

Lấy P(x):Q(x)=2x-7 dư a+21

Vậy để P(x)⋮Q(x) ⇒ a+21=0 ⇒ a=-21

c) P(x)=x³+ax²-4; Q(x)=x²+4x+4

Lấy P(x):Q(x)=x+a-4 dư -4(a-5)x+12

Vậy để P(x)⋮Q(x) ⇒ -4(a-5)x+12=0 ⇒ (a-5)x=3

⇒ a-5 ϵ {-1;1;-3;3} (a ϵ Z)

⇒ a ϵ {4;6;2;8}

d) P(x)=2x²+ax+1; Q(x)=x-3

Lấy P(x):Q(x)=2x+a+6 dư 3a+19

Vậy để P(x)⋮Q(x) ⇒ 3a+19=0 ⇒ a=-19/3

e) P(x)=ax⁵+5x⁴-9; Q(x)=x-1

Lấy P(x):Q(x)=ax⁴+(a-5)x³+(a-5)x²+(a-5)x+1 dư a-4

Vậy để P(x)⋮Q(x) ⇒ a-4=0 ⇒ a=4

f) P(x)=6x³-x²-23x+a; Q(x)=2x+3

Lấy P(x):Q(x)=3x²-5x-4 dư a+12

Vậy để P(x)⋮Q(x) ⇒ a+12=0 ⇒ a=-12

g) P(x)=x³-6x²+ax-6 Q(x)=x-2

Lấy P(x):Q(x)=x²-2x+a-4 dư 2(a-4)-6

Vậy để P(x)⋮Q(x) ⇒ 2(a-4)-6=0 ⇒ a=7

Bài h có a,b bạn xem lại đề

Lời giải:

a.

PT $\Leftrightarrow 3x^2+\frac{x}{2}-3x^2+3x+2=0$
$\Leftrightarrow \frac{7}{2}x+2=0$
$\Leftrightarrow \frac{7}{2}x=-2$
$\Leftrightarrow x=-2: \frac{7}{2}=\frac{-4}{7}$
b.

PT $\Leftrightarrow 5x^2-3-5x^2-6x=0$

$\Leftrightarrow -3-6x=0$

$\Leftrightarrow 6x=-3$

$\Leftrightarrow x=\frac{-3}{6}=\frac{-1}{2}$

\(a\\ -5x^2+3x.\left(x+2\right)=-5x^2+3x^2+6x=-2x^2+6x\\ b\\ -2x.\left(1-x^2\right)-2x^3=-2x+2x^3-2x^3=-2x\\ c\\ 4x.\left(x-1\right)-4.\left(x^2+2x-1\right)\\ =4x^2-4x-4x^2-8x+4=-12x+4\)

\(d\\ 6x^3-2x^2.\left(-x^2-3x\right)=6x^3+2x^4+6x^3=2x^4+12x^3\\ e\\ 3x.\left(x-1\right)-\left(1+2x\right).5x\\ =3x^2-3x-5x-10x^2=-7x^2-8x\\ f\\ -5x^2-\left(x-6\right).\left(-2x^2\right)=-5x^2+2x^3-12x^2=2x^3-17x^2\)

`@` `\text {Ans}`

`\downarrow`

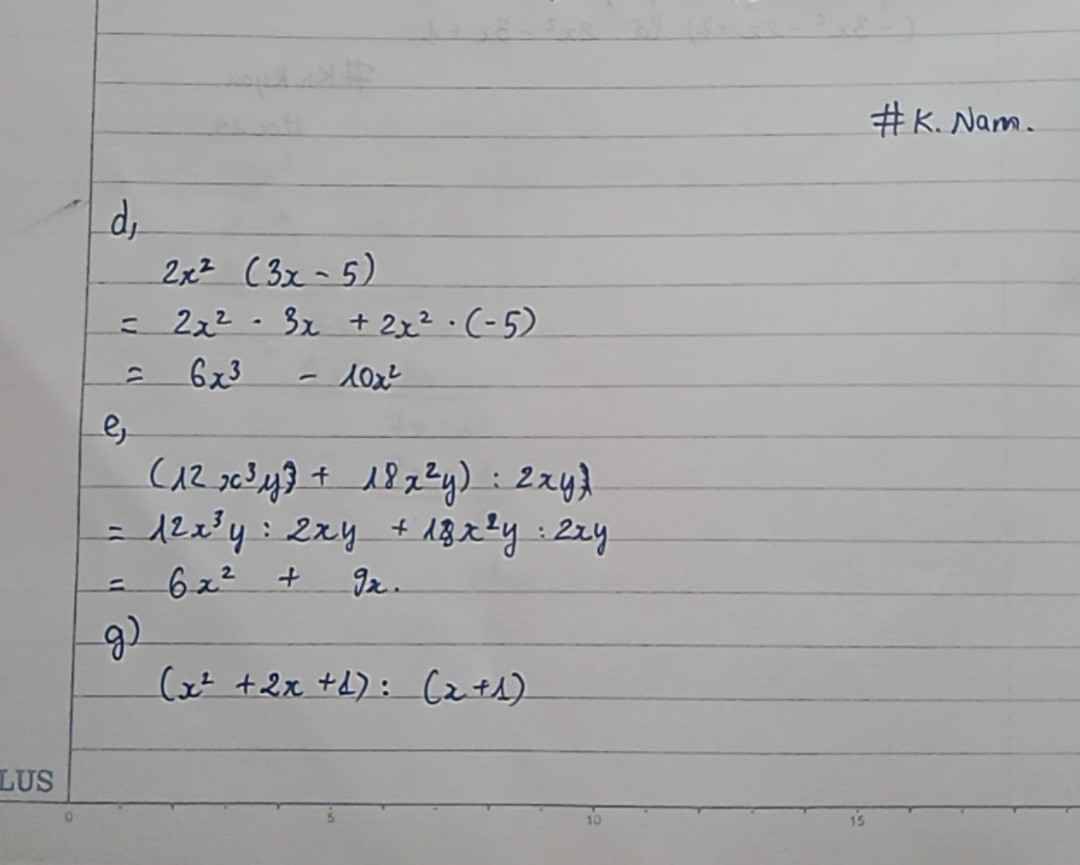
^{*Máy tớ cam hơi mờ, cậu thông cảm ._.*}

Cậu viết lại rõ đề câu c, nhé.

\(a,N\left(x\right)=x^2+3x^4-2x-x^2+2x^3=3x^4+2x^3+\left(x^2-x^2\right)-2x\\ =3x^4+2x^3-2x\\ P\left(x\right)=-8+5x-6x^3-4x+6=-6x^3+\left(5x-4x\right)+\left(-8+6\right)\\ =-6x^3+x-2\)

Bậc của N(x) là 4

Bậc của P(x) là 3

\(b,P\left(x\right)+N\left(x\right)=3x^4+2x^3-2x-6x^3+x-2\\ =3x^4+\left(2x^3-6x^3\right)+\left(-2x+x\right)-2\\ =3x^4-4x^3-x-2\)

\(c,B\left(x\right)=-2x^2\left(x^3-2x+5x^2-1\right)\\ =\left(-2x^2\right).x^3+\left(-2x^2\right).\left(-2x\right)+\left(-2x^2\right).5x^2+\left(-2x^2\right).\left(-1\right)\\ =-2x^5+4x^3-10x^4+2x^2\\ =-2x^5-10x^4+4x^3+2x^2\)

\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)

Bn viết kiểu gì vậy,6x3 là 18x hay là 6x\(^3\)

a: \(P\left(x\right)=6x^3-x-1+5x^3+x^2-2x-1=11x^3+x^2-3x-2\)

b: \(Q\left(x\right)=6x^3-x-1-5x^3-x^2+2x+1=x^3-x^2+x\)

c: \(2\cdot U\left(x\right)=5x^3-2x+x^2-1-3\cdot\left(6x^3-x-1\right)\)

\(\Leftrightarrow2\cdot U\left(x\right)=5x^3+x^2-2x-1-18x^3+3x+3\)

\(\Leftrightarrow2\cdot U\left(x\right)=-13x^3+x^2+x+2\)

hay \(U\left(x\right)=-\dfrac{13}{2}x^3+\dfrac{1}{2}x^2+\dfrac{1}{2}x+1\)

\(a,P\left(x\right)=A\left(x\right)+B\left(x\right)=6x^3-x-1+5x^3-2x+x^2-1=11x^3+x^2+x-2\)

\(b,Q\left(x\right)=A\left(x\right)-B\left(x\right)=6x^3-x-1-5x^3+2x-x^2+1=x^3-x^2+x\)

c, Ta có : \(2U\left(x\right)+2A\left(x\right)=B\left(x\right)\)

hay   \(2U\left(x\right)+2\left(6x^3-x-1\right)=5x^3-2x+x^2-1\)

\(\Rightarrow2U\left(x\right)+12x^3-2x-2=5x^3-2x+x^2-1\)

\(\Rightarrow2U\left(x\right)=5x^3-2x+x^2-1-12x^3+2x+2\)

\(\Rightarrow U\left(x\right)=-7x^3+x^2+1\)