1.Quan sát xung quanh và chỉ ra những đồ vật có trục đối xứng mà em biết,chẳng hạn:tam giác đều;hình tròn;hay một số chữ cái in hoa

Những câu hỏi liên quan
Nhận biết nguyên tố hóa học có mặt xung quanh taChuẩn bị: các mẫu đồ vật (hộp sữa, dây đồng, đồ dùng học tập,…)Quan sát các đồ vật đã chuẩn bị, thảo luận nhóm và thực hiện yêu cầu:1. Hãy đọc tên những nguyên tố hóa học mà em biết trong các đồ vật trên.2. Viết kí hiệu hóa học và nêu một số ứng dụng của những nguyên tố hóa học đó.
Đọc tiếp
Nhận biết nguyên tố hóa học có mặt xung quanh ta
Chuẩn bị: các mẫu đồ vật (hộp sữa, dây đồng, đồ dùng học tập,…)
Quan sát các đồ vật đã chuẩn bị, thảo luận nhóm và thực hiện yêu cầu:
1. Hãy đọc tên những nguyên tố hóa học mà em biết trong các đồ vật trên.
2. Viết kí hiệu hóa học và nêu một số ứng dụng của những nguyên tố hóa học đó.
- Dây đồng: Copper.
+ Kí hiệu hóa học: Cu
+ Ứng dụng: Làm dây điện, đúc tượng, đúc chuông, chi tiết máy, chế tạo các thiết bị dùng trong công nghiệp đóng tàu biển
- Thước nhôm: Aluminium
+ Kí hiệu hóa học: Al
+ Ứng dụng: làm xoong, nồi; làm vật liệu chế tạo máy bay, ô tô, tên lửa…; trang trí nội thất; hàn đường ray
Đúng 1
Bình luận (0)
Quan sát xung quanh và chỉ ra được những hình ảnh có liên quan đến : tia , tia phân biệt , tia chung gốc , tia đối nhau
Quan sát những hình dưới đây và cho biết:
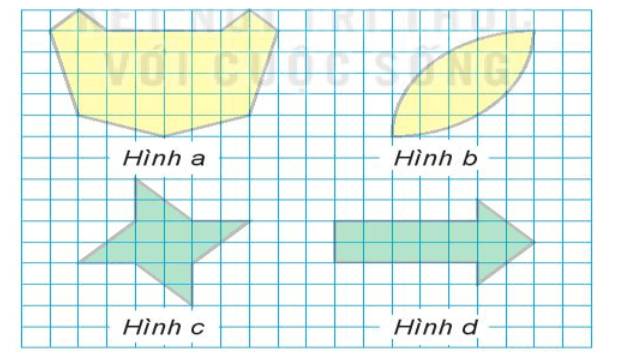
a) Hình nào không có trục đối xứng?
b) Hình nào chỉ có một trục đối xứng?
c) Hình nào có hai trục đối xứng?
a) Hình không có trục đối xứng: hình c
b) Hình chỉ có một trục đối xứng: hình d, hình a
c) Hình có hai trục đối xứng: hình b
Đúng 0
Bình luận (0)
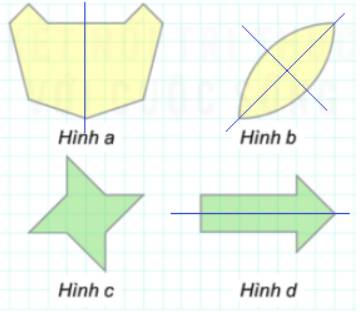
a) Hình c) không có trục đối xứng.
b) Hình a) và hình d) có đúng một trục đối xứng
c) Hình b) có hai trục đối xứng.
Đúng 0
Bình luận (0)
1. Bằng cách gấp giấy, em hãy tìm một trục đối xứng của đoạn thẳng.
2. Làm tương tự như HĐ 6 với hình tam giác đều, hình vuông, hình lục giác đều. Em hãy chỉ ra một trục đối xứng của mỗi hình trên.
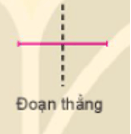
1. Thực hành gấp giấy: Vẽ đoạn thẳng trên tờ giấy, gấp tờ giấy theo một đường thẳng sao cho 2 đầu đoạn thẳng trùng nhau thì đường thẳng đó là một trục đối xứng.
+) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
2.
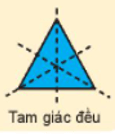
+) Trục đối xứng của tam giác đều là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện (có 3 trục đối xứng)
+) Trục đối xứng của hình vuông là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông (có 4 trục đối xứng)
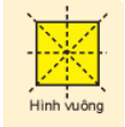
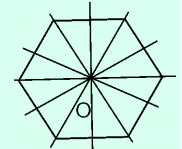
+) Trục đối xứng của lục giác đều là đường thẳng nối 1 đỉnh và tâm của lục giác đều (có 6 trục đối xứng).
Đúng 1
Bình luận (0)
a) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
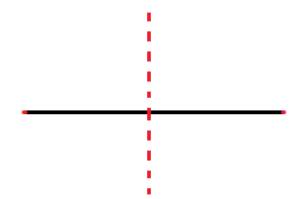
b)
+ Tam giác đều có 3 trục đối xứng là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện
+ Hình vuông có 4 trục đối xứng là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông
+ Hình lục giác đều có 6 trục đối xứng.
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:
1. Tam giác đều có 3 trục đối xứng và 1 tâm đối xứng
2. Hình vuông có 4 trục đối xứng và 1 tâm đối xứng
3. Ngũ giác đều có 5 trục đối xứng và 1 tâm đối xứng
4. Lục giác đều có 6 trục đối xứng và 1 tâm đối xứng
Số mệnh đềđúng là:
A.1
B.2
C.3
D.4
Quan sát môi trường xung quanh nhà, trường học…) sau đó hãy nêu tên một vài cây, con vật, đồ vật mà em biết. Sau đó hãy chọn ra mỗi loại ví dụ để trao đổi và thảo luận. VD: Cây đậu con Con gà con Hòn đá. Em hãy cho biết - Con gà, cây đậu cần những điều kiện gì để sống ? - Hòn đá (viên gạch, cái bàn,...) có cần những điều kiện giống như con gà, cây đậu để tồn tại hay không? - Con gà, cây đậu có lớn lên sau một thời gian được nuôi trồng hay không? Trong khi đó hòn đá có tăng kích thước không? ...
Đọc tiếp
Quan sát môi trường xung quanh nhà, trường học…) sau đó hãy nêu tên một vài cây, con vật, đồ vật mà em biết. Sau đó hãy chọn ra mỗi loại ví dụ để trao đổi và thảo luận.
VD: Cây đậu con
Con gà con
Hòn đá.
Em hãy cho biết
- Con gà, cây đậu cần những điều kiện gì để sống ?
- Hòn đá (viên gạch, cái bàn,...) có cần những điều kiện giống như con gà, cây đậu để tồn tại hay không?
- Con gà, cây đậu có lớn lên sau một thời gian được nuôi trồng hay không? Trong khi đó hòn đá có tăng kích thước không?
- Từ những điều trên, em hãy nêu những đặc điểm khác nhau giữa vật sống và vật không sống.
- Con gà, cây đậu cần ánh sáng, nước, chất dinh dưỡng (thức ăn, phân bón, ...), không khí,... để sống.
- Hòn đá không cần các điều kiện giống như con gà, cây đậu.
- Sau một thời gian nuôi trồng, cây đậu, con gà lớn lên. Hòn đá thì không có sự thay đổi kích thước.
- Những điểm khác nhau của vật sống và vật không sống: Vật sống có sự trao đổi chất với môi trường (lấy chất cần thiết và loại bỏ các chất thải ra ngoài ), có sự lớn lên, sinh sản.
Đúng 0
Bình luận (0)
Tính đối xứng là một yếu tố tạo nên sự cân đối, hài hòa của các hình. Tuy nhiên, không phải lúc nào ta cũng có thể gấp hình để biết hình có trục đối xứng hay không. Em hãy quan sát và vẽ phác trục đối xứng của hình Tháp Chàm và ngôi sao sáu cánh dưới đây (nếu có).

Ta có thể kẻ trục đối xứng của hai hình như sau:

Đúng 0
Bình luận (0)
Các phát biểu nào sai?
A. Hình tròn có vô số trục đối xứng và 1 tâm đối xứng
B. Hình vuông có 4 trục đối xứng
C. Hình tam giác đều có 3 trục đối xứng 1 tâm đối xứng
D. Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
Đúng 0
Bình luận (0)
vẽ tâm đối xứng , trục đối xứng của tam giác cân , tam giác đều ( nếu không có thì hãy chỉ rõ và giải thích )
SGK ... Tam giác cân không có tâm đối xứng đâu... Trục đối xứng của tam giác cân là ... Khó nói quá . VD nha : tam giác ABC cân tại A TH1 : kẻ AH vuông góc với BC => AH là trục đối xứng ( CM được tam giác ABH = ACH => ĐPCM) (1)
TH2 : Kẻ trung tuyến AI vì tam giác ABC cân tại A nên => AI vừa là trung tuyến vừa là đường cao => Tương tự (1)
Nhớ được các trường hợp đặc biệt của các đường trung tuyến, phân giác, đường cao ..v..v... trong tam giác cân thì cứ biện luận thôi, không cần phải giải thích nhiều vì ta công nhận điều đó là đúng ...
Đúng 0
Bình luận (0)




















