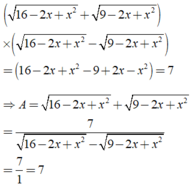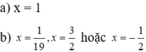Chọn đáp án D.

Ta có:

1. \(2^x-26=6\)

\(\Rightarrow2^x=6+26\)

\(\Rightarrow2^x=32\)

\(\Rightarrow2^x=2^5\)

\(\Rightarrow x=5\)

2. \(64\cdot4^x=16^8\)

\(\Rightarrow4^3\cdot4^x=4^{16}\)

\(\Rightarrow4^x=4^{16}:4^3\)

\(\Rightarrow4^x=4^{13}\)

\(\Rightarrow x=13\)

3. \(\left(2x-1\right)^4=16\)

\(\Rightarrow\left(2x-1\right)^4=2^4\)

\(\Rightarrow2x-1=2\)

\(\Rightarrow2x=3\)

\(\Rightarrow x=\dfrac{3}{2}\)

4. \(\left(2x+1\right)^3=125\)

\(\Rightarrow\left(2x+1\right)^3=5^3\)

\(\Rightarrow2x+1=5\)

\(\Rightarrow2x=4\)

\(\Rightarrow x=2\)

       \(2x-9\)\(⋮\)\(x-5\)

\(\Leftrightarrow\)\(2\left(x-5\right)+1\)\(⋮\)\(x-5\)

Ta thấy     \(2\left(x-5\right)\)\(⋮\)\(x-5\)

\(\Rightarrow\)\(1\)\(⋮\)\(x-5\)

\(\Rightarrow\)\(x-5\)\(\inƯ\left(1\right)=\left\{-1;1\right\}\)

\(\Rightarrow\)\(x=\left\{4;6\right\}\)

bài cần bổ xung thêm x ∈ Z hoặc x ∈ N chứ bn!

ta có:

2x - 9 ⋮ x - 5

=> (2x-10) + 10 - 9 ⋮ x - 5

=> (2x-2.5) + 1 ⋮ x - 5

=> 2(x-5) + 1 ⋮ x - 5

có x - 5 ⋮ x - 5 => 2(x-5) ⋮ x - 5

=> 1 ⋮ x - 5

=> x - 5 ∈ Ư(1)

x ∈ Z => x - 5 ∈ Z

=> x - 5 ∈ {-1;1}

=> x  ∈ {4;6}

vậy____

Câu hỏi là Tìm các số nguyên x sao cho: 2x-9 chia hết cho x-5 đúng ko?

1.

PT $\Leftrightarrow 2^{x^2-5x+6}+2^{1-x^2}-2^{7-5x}-1=0$

$\Leftrightarrow (2^{x^2-5x+6}-2^{7-5x})-(1-2^{1-x^2})=0$

$\Leftrightarrow 2^{7-5x}(2^{x^2-1}-1)-(2^{x^2-1}-1)2^{1-x^2}=0$

$\Leftrightarrow (2^{x^2-1}-1)(2^{7-5x}-2^{1-x^2})=0$

$\Rightarrow 2^{x^2-1}-1=0$ hoặc $2^{7-5x}-2^{1-x^2}=0$

Nếu $2^{x^2-1}=1\Leftrightarrow x^2-1=0$

$\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$

$2^{7-5x}-2^{1-x^2}=0$

$\Leftrightarrow 7-5x=1-x^2\Leftrightarrow x^2-5x+6=0$

$\Leftrightarrow (x-2)(x-3)=0\Leftrightarrow x=2; x=3$

2. Đặt $\sin ^2x=a$ thì $\cos ^2x=1-a$. PT trở thành:

$16^a+16^{1-a}=10$

$\Leftrightarrow 16^a+\frac{16}{16^a}=10$

$\Leftrightarrow (16^a)^2-10.16^a+16=0$

Đặt $16^a=x$ thì:

$x^2-10x+16=0$

$\Leftrightarrow (x-2)(x-8)=0$

$\Leftrightarrow x=2$ hoặc $x=8$

$\Leftrightarrow 16^a=2$ hoặc $16^a=8$

$\Leftrightarrow 2^{4a}=2$ hoặc $2^{4a}=2^3$

$\Leftrightarroww 4a=1$ hoặc $4a=3$

$\Leftrightarrow a=\frac{1}{4}$ hoặc $a=\frac{3}{4}$

Nếu $a=\frac{1}{4}\Leftrightarrow \sin ^2x=\frac{1}{4}$

$\Leftrightarrow \sin x=\pm \frac{1}{2}$

Nếu $a=\sin ^2x=\frac{3}{4}\Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$

Đến đây thì đơn giản rồi.

2x-1*1-2x=-16

2x-1-2x=-16

2x-2x-1=-16

0-1=-16

suy ra ko có x thỏa mãn

đặt A=2^x +2^x+1 +.....+2^x+2021=2^x+2026-16

đặt 2A = 2^x+1 +2^x+2 +......+2^x+2022=2^x+2027-32

lấy 2A-A =2^x+2022-2^x=2^2026-16

vậy,ta suy ra x=4

=>\(2^x\left(1+2+2^2+...+2^{2021}\right)=2^4\left(2^{2022}-1\right)\)

=>2^x=2^4

=>x=4

Đặt \(A=2^x+2^{x+1}+...+2^{x+2021}=2^{x+2026-16}\)

Đặt \(2A=2^{x+1}+2^{x+2}+...+2^{x+2022}=2^{x+2027+32}\)

Ta lấy \(2A-A=2^{x+2022}-2^x=2^{2026-16}\)

\(\Rightarrow x=4\)

Vậy \(x=4\)

\(2VT=2^{x+1}+2^{x+2}+2^{x+3}+...+2^{x+2022}\)

\(VT=2VT-VT=2^{x+2022}-2^x\)

\(\Rightarrow2^{x+2022}-2^x=2^{2026}-16\)

\(\Leftrightarrow2^{2022}.2^x-2^x=2^{2026}-2^4\)

\(\Leftrightarrow2^x\left(2^{2022}-1\right)=2^4\left(2^{2022}-1\right)\)

\(\Leftrightarrow2^x=2^4\Rightarrow x=4\)

\(2^x+2^{x+1}+2^{x+2}+...+2^{x+2021}=2^{2026}-16\)

\(\Rightarrow2^x\left(1+2^x+2^{x+1}+...+2^{x+2020}\right)=2^{2026}-2^4\)

\(\Rightarrow2^x.\dfrac{2^{x+2020+1}-1}{2-1}=2^4.\left(2^{2022}-1\right)\)

\(\Rightarrow2^x.\left(2^{x+2021}-1\right)=2^4.\left(2^{2022}-1\right)\)

\(\Rightarrow x\in\varnothing\)