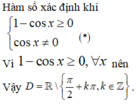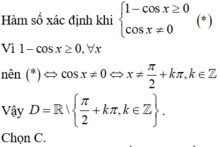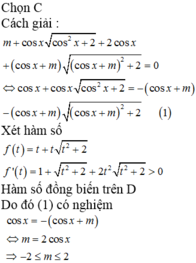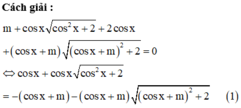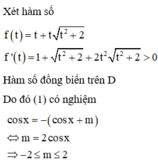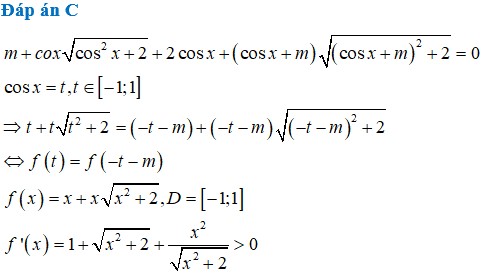cosxcos2x=cos3x

Những câu hỏi liên quan
1)Giải pt bậc hai đối với một hàm số lượng giác:
a. 2 cosxcos2x=1+cos2x+cos3x
b.5(1+cosx)=2+sin^4x-cos^4x
c.sin^4x +cos^4x=sin2x-1/2
2) giải phương trình chứa ẩn dưới mẫu:
Sin2x+2cosx-sinx-1/ tan x+√3=0
Tập xác định của hàm số
y
1
-
cos
x
cos
2
x
là: B. D R
Đọc tiếp
Tập xác định của hàm số y = 1 - cos x cos 2 x là:
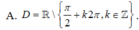
B. D= R
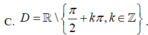
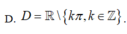
Tập xác định của hàm số
y
1
-
cos
x
cos
2
x
là: B. DR
Đọc tiếp
Tập xác định của hàm số y = 1 - cos x cos 2 x là:
![]()
B. D=R
![]()
![]()
Cho phương trình
1
+
cos
x
c
os
2
x
−
cos
x
−
sin
2
x
cos...
Đọc tiếp
Cho phương trình 1 + cos x c os 2 x − cos x − sin 2 x cos x + 1 = 0. Tính tổng tất cả các nghiệm năm trong khoảng 0 ; 2018 π của phương trình đã cho?
A. 1019090 π
B. 2037171 π
C. 2035153 π
D. 1017072 π
Đáp án D
ĐK: cos x ≠ − 1 . Khi đó P T ⇔ 1 + cos x 2 c os 2 x − cos x − 1 − 1 − c os 2 x 1 + cos x = 0
⇔ 2 c os 2 x − cos x − 1 − 1 − cos x = 0 ⇔ 2 c os 2 x = 2 ⇔ cos x = 1 cos x = − 1 ( l o a i ) ⇔ x = k 2 π
Do x ∈ 0 ; 2018 ⇒ k ∈ 1 ; 1008 ⇒ ∑ = 1 + 2 + 3 + ... + 1008 .2 π = 1 + 1008 2 .1008.2 π = 1017072 π
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực
m
+
cos
x
cos
2
x
+
2
+
2
cos
x
+
cos
x
+
m
cos
x
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực m + cos x cos 2 x + 2 + 2 cos x + cos x + m cos x + m 2 + 2 = 0
A. 3
B. 4
C. 5
D. 6
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực ?
m
+
cos
x
cos
2
x
+
2
+
2
cos
x
+
cos
x
+
m
cos
x
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực ?
m + cos x cos 2 x + 2 + 2 cos x + cos x + m cos x + m 2 + 2 = 0
A. 3
B. 4
C. 5
D. 6
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m
+
c
o
s
x
c
o
s
2
x
+
2
+
2
c
o
s
x
+
(
c
o
s
x
+
m
)
(
c
o...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình m + c o s x c o s 2 x + 2 + 2 c o s x + ( c o s x + m ) ( c o s x + m ) 2 + 2 = 0 có nghiệm thực
A. 3
B. 4
C. 5
D. 6
sin3x(cosx - sin3x) + cos3x(sinx - cos3x)= 0
\(sin3x\left(cosx-sin3x\right)+cos3x\left(sinx-cos3x\right)=0\\ \Leftrightarrow sin3x\cdot cosx+cos3x\cdot sinx=sin^23x+cos^23x\\ \Leftrightarrow sin4x=1=sin\frac{\pi}{2}\\ \Leftrightarrow4x=\frac{\pi}{2}+k2\pi\\ \Leftrightarrow x=\frac{\pi}{8}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
cos2x + cos4x + cos6x = 0
1 + cosx + cos2x + cos3x = 0
sin3x - sinx = cos3x - cosx
a. cos2x + cos4x + cos6x = 0
\(\Leftrightarrow\left(cos2x+cos6x\right)+cos4x=0\\ \Leftrightarrow2cos4x.cos2x+cos4x=0\\ \Leftrightarrow cos4x\left(2cos2x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=\dfrac{-1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=\pm\dfrac{\pi}{3}+k\pi\end{matrix}\right.\left(k\in Z\right)}\)
Đúng 0
Bình luận (0)
1.
\(cos2x+cos6x+cos4x=0\)
\(\Leftrightarrow2cos4x.cos2x+cos4x=0\)
\(\Leftrightarrow cos4x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\2x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=\pm\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
\(\Leftrightarrow1+cos2x+cosx+cos3x=0\)
\(\Leftrightarrow1+2cos^2x-1+2cos2x.cosx=0\)
\(\Leftrightarrow cos^2x+cos2x.cosx=0\)
\(\Leftrightarrow cosx\left(cos2x+cosx\right)=0\)
\(\Leftrightarrow cosx\left(2cos^2x+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=-1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pi+k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời