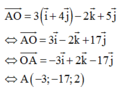Trong hệ trục tọa độ (0.vecto i;j), cho hình vuông abcd tâm I và có A(1,3).Biết điểm B thuộc trục (0.vecto i) và vecto BC cùng hướng với i .Tìm tọa độ các vecto AB,AC,BC

Những câu hỏi liên quan
Trong hệ trục tọa độ (O, vecto i, vecto j) cho 2 vécto vecto a=2 vecto i - 4 vecto j ; vecto b=-5 vecto i + 3 vecto j. Tọa độ của vecto u=2 vecto a - vecto b là
\(\overrightarrow{a}=2\overrightarrow{i}-4\overrightarrow{j}\Rightarrow\overrightarrow{a}=\left(2;-4\right)\)
\(\overrightarrow{b}=-5\overrightarrow{i}+3\overrightarrow{j}\Rightarrow\overrightarrow{b}=\left(-5;3\right)\)
\(\Rightarrow\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}=2\left(2;-4\right)-\left(-5;3\right)=\left(9;-11\right)\)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho
a
→
-
i
→
+
2
j
→
-
3
k
→
Tọa độ của vecto
a
→
là A. (2;-1;-3) B. (-3;2;-1) C. (-1;2;-3) D. (2;-3;-1)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho a → = - i → + 2 j → - 3 k → Tọa độ của vecto a → là
A. (2;-1;-3)
B. (-3;2;-1)
C. (-1;2;-3)
D. (2;-3;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho a → = − i → + 2 j → − 3 k → . Tọa độ của vecto a → là
A. (2;-1;-3)
B. (-3;2;-1)
C. (-1;2;-3)
D. (2;-3;-1)
Trong không gian với hệ trục tọa độ Oxyz cho vecto
A
O
→
3
(
i
→
+
4
j
→
)
-
2
k
→
+
5
j
→
. Tìm tọa độ điểm A. A. A(3;5;-2) B. A(-3;-17;2) C. A(-3;17;-2) D. A(3;-2;5)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho vecto A O → = 3 ( i → + 4 j → ) - 2 k → + 5 j → . Tìm tọa độ điểm A.
A. A(3;5;-2)
B. A(-3;-17;2)
C. A(-3;17;-2)
D. A(3;-2;5)
Trong không gian với hệ trục tọa độ Oxyz cho vecto
A
O
→
3
(
i
→
+
4
j
→
)
-
2
k
→
+
5
j
→
. Tìm tọa độ điểm A
A
.
A
(
3
;
5
;...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho vecto A O → = 3 ( i → + 4 j → ) - 2 k → + 5 j → . Tìm tọa độ điểm A
A . A ( 3 ; 5 ; - 2 )
B . A ( - 3 ; - 17 ; 2 )
C . A ( - 3 ; 17 ; - 2 )
D . A ( 3 ; - 2 ; 5 )
Trong hệ trục tọa độ Oxyz cho mặt phẳng (P) x-4y+3z-2=0. Một vecto pháp tuyến của (P)
A. (0;-4;3)
B. (1;4;3)
C. (-1;4;-3)

Trong không gian với hệ trục tọa độ Oxyz, một vecto pháp tuyến của mặt phẳng α : x-2y+3z+1=0
A. (3;-2;1)
B. (1;-2;3)
C. (1;2;-3)
D. (1;-2;-3)
Trong hệ trục tọa độ Oxyz, cho phương trình mặt phẳng (P): x-2y+3=0. Vecto pháp tuyến của (P) là
A. (1;-2;3)
B. (1;-2;0)
C. (1;-2)
D. (1;3)
Câu 1: Trong hệ trục (O,overrightarrow{i},overrightarrow{j}), tọa độ overrightarrow{i}-overrightarrow{j}làCâu 2:Cho overrightarrow{a}(3;-4), overrightarrow{b}(-1;2). Tọa độ vecto overrightarrow{a}+2overrightarrow{b}là
Đọc tiếp
Câu 1: Trong hệ trục (O,\(\overrightarrow{i}\),\(\overrightarrow{j}\)), tọa độ \(\overrightarrow{i}\)-\(\overrightarrow{j}\)là
Câu 2:Cho \(\overrightarrow{a}\)(3;-4), \(\overrightarrow{b}\)(-1;2). Tọa độ vecto \(\overrightarrow{a}\)+2\(\overrightarrow{b}\)là
Lời giải:
$\overrightarrow{i}=(1,0), \overrightarrow{j}=(0,1)$
$\Rightarrow \overrightarrow{i}-\overrightarrow{j}=(1-0,0-1)=(1,-1)$
Đúng 1
Bình luận (0)
Bài 2:
$\overrightarrow{a}+2\overrightarrow{b}=(3+2.-1, -4+2.2)=(1, 0)$
Đúng 1
Bình luận (0)