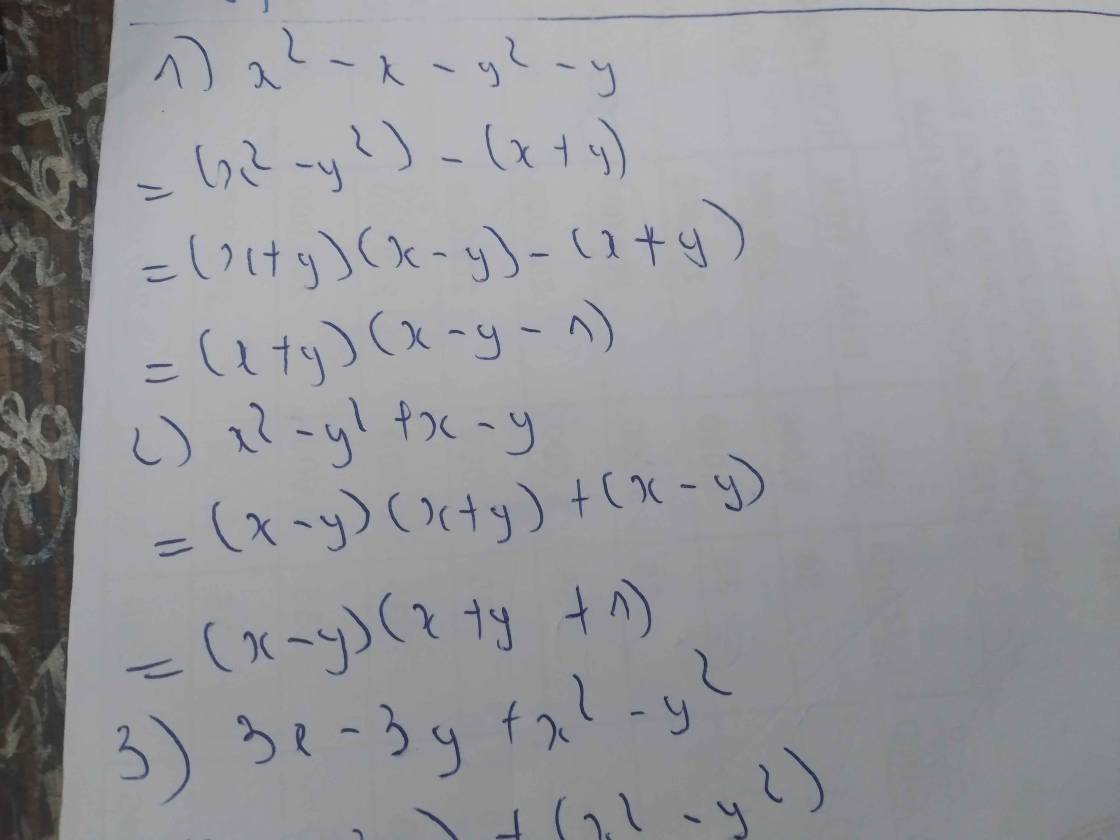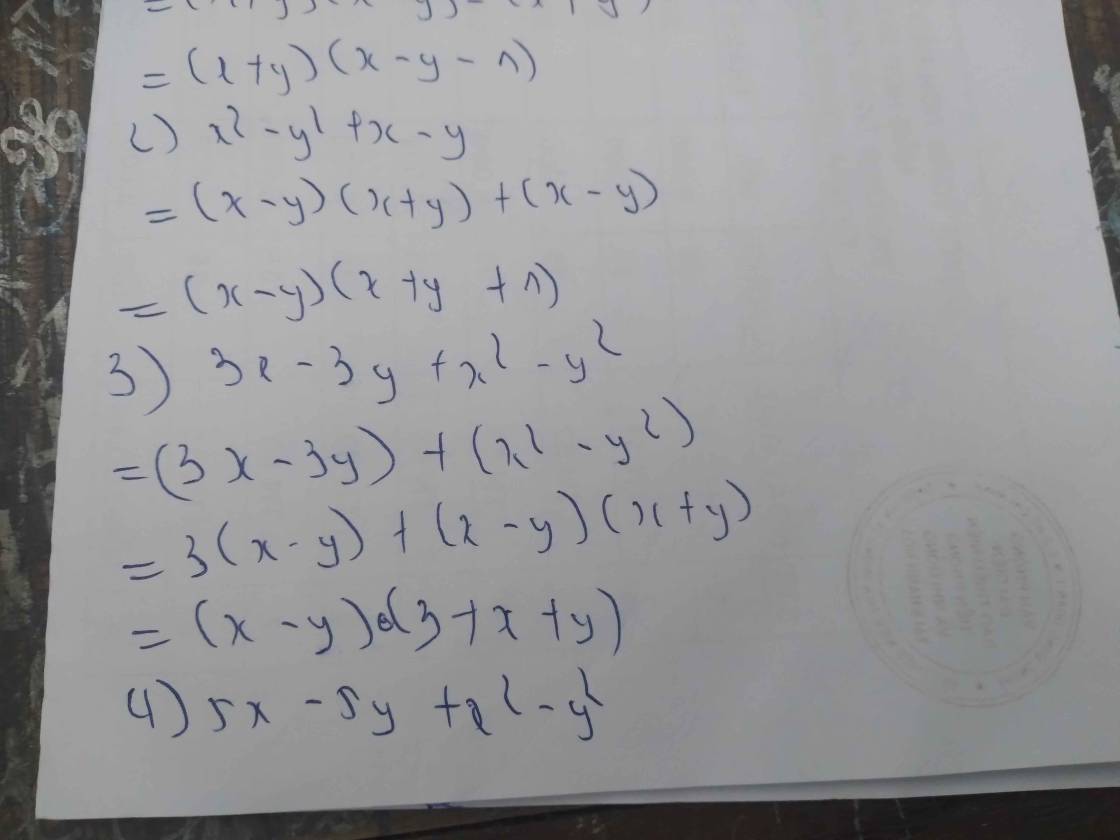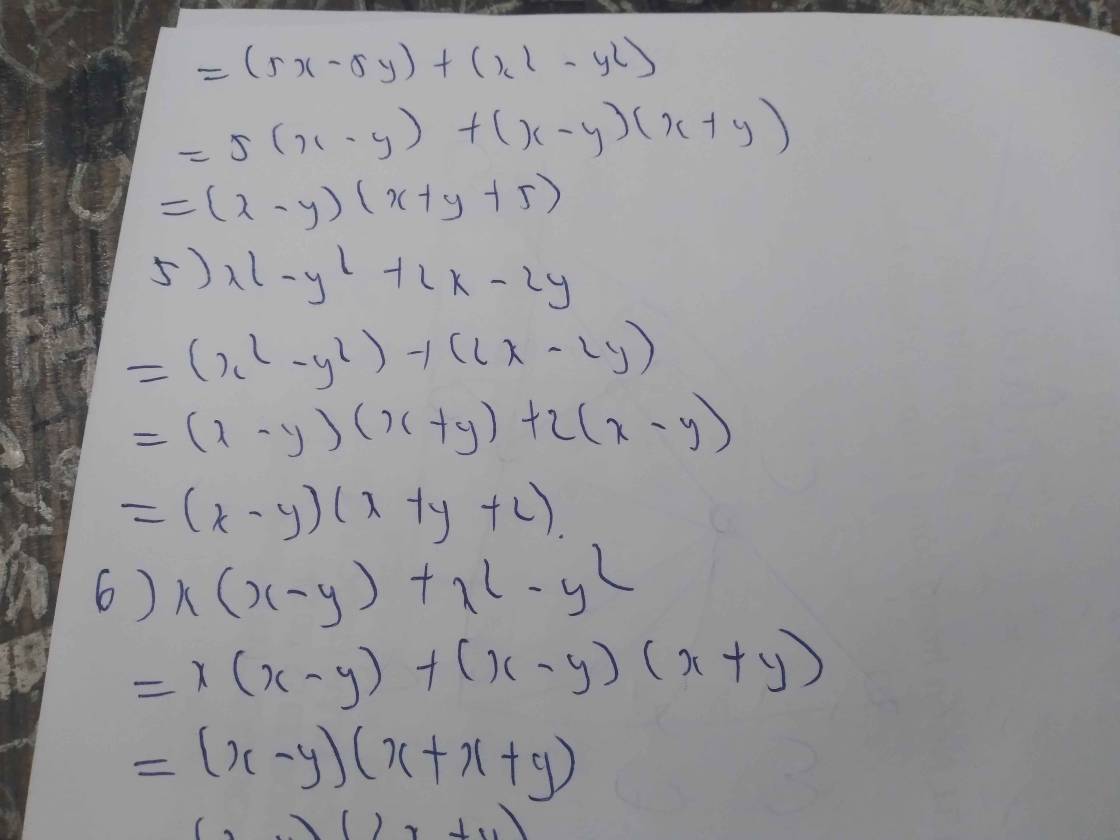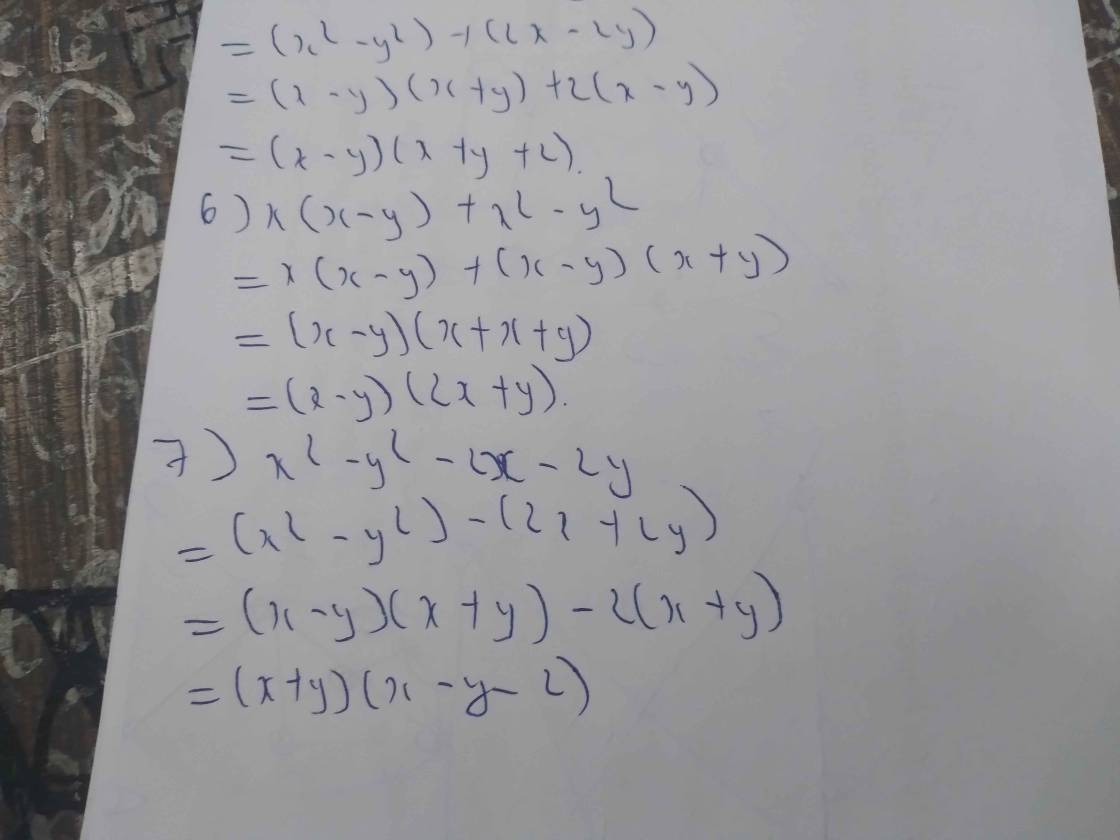( x + y )2 + 2( x + y ) (x - y ) + ( x - y )2

Những câu hỏi liên quan
Chọn câu sai. A.x^2-y^2=(x+y)(x-y) B.(x+y)(x+y)=y^2-x^2 C.(x+y)^2=(x+y)(x-y) D.(-x-y)^2=(-x)^2-2(-x)y+y^2
a/ \(\dfrac{x^2}{x^2-y^2}\) - \(\dfrac{2\text{x}y}{x^2-y^2}\) + \(\dfrac{y^2}{x^2-y^2}\)
b/ \(\dfrac{x+y}{x-y}\) - \(\dfrac{x-y}{x+y}\) - \(\dfrac{4y^2}{x^2-y^2}\)
giúp mình với huhu mình cần gấp
\(a,=\dfrac{x^2-2xy+y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x-y}{x+y}\\ b,=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2-4y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{4xy-4y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{4y\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{4y}{x+y}\)
Đúng 4
Bình luận (0)
a.\(\dfrac{\left(x-y\right)^2}{x^2-y^2}\)
b.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Rút gon
A= (x−y)^2+(x+y)^2+(x−y)(x+y)
B=(x−y)^2+(−x+y−z)^2+2(x−y)(−x+y−z)
\(A=x^2-2xy+y^2+x^2+2xy+y^2+x^2-y^2=3x^2+y^2\\ B=\left(x-y-x+y-z\right)^2=\left(-z\right)^2=z^2\)
Đúng 1
Bình luận (1)
Bài 1 : Phân tích thành nhân tử 1) x^2 - x - y^2 - y 2) x^2 - y^2 +x - y 3) 3x - 3y + x^2 - y^2 4) 5x - 5y + x^2 - y^2 5) x^2 - y^2 + 2x -2y 6) x( x-y) + x^2 - y^2 7) x^2 - y^2 - 2x -2y
Rút gọn biểu thức:
a) (x+y)^2+(x-y)^2+(x+y).(x-y)
b) (3x+y)^2+(x-3y)2-(2x+y).(2x-y)
c) 2(x-y).(x+y)+(x+y)^2+(x-y)^2
d)-2(x^2-9y^2)+(x-3y)^2+(x+3y)^2
a) \(\left(x+y\right)^2+\left(x-y\right)^2+\left(x+y\right)\left(x-y\right)\)
\(=x^2+2xy+y^2+x^2-2xy+y^2+x^2-y^2\)
\(=3x^2+y^2\)
b)\(\left(3x+y\right)^2+\left(3x-y\right)^2-\left(2x+y\right)\left(2x-y\right)\)
\(=9x^2+6xy+y^2+9x^2-6xy+y^2-4x^2+y^2\)
\(=14x^2+3y^2\)
c) \(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left(x-y+x+y\right)^2\)
\(=4x^2\)
d)\(-2\left(x^2-9y^2\right)+\left(x-3y\right)^2+\left(x+3y\right)^2\)
\(=\left(x+3y\right)^2-2\left(x+3y\right)\left(x-3y\right)+\left(x-3y\right)^2\)
\(=\left(x+3y-x+3y\right)^2=9y^2\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức
a,(x+y)2-(x-y)2
b,(x-y-z)2+(x+y+z)2
c,(x+y)2-2(x+y)(x-y)+(x-y)2
\(\left(a\right):\left(x+y\right)^2-\left(x-y\right)^2=x^2+2xy+y^2-\left(x^2-2xy+y^2\right)\\ =x^2+2xy+y^2-x^2+2xy-y^2\\ =4xy\)
\(\left(b\right):\left(x-y-z\right)^2+\left(x+y+z\right)^2\\ =\left[\left(x-y\right)-z\right]^2+\left[\left(x+y\right)+z\right]^2\\ =\left(x-y\right)^2-2z\left(x-y\right)+z^2+\left(x+y\right)^2+2z\left(x+y\right)+z^2\\ =x^2-2xy+y^2-2xz+2yz+z^2+x^2+2xy+y^2+2xz+2yz+z^2\\ =2x^2+2y^2+2z^2+4yz\)
\(\left(c\right):\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =\left(2y\right)^2=4y^2\)
Đúng 2
Bình luận (0)
rút gọn B=(x+y)^3 +3(x-y)(x+y)^2+3(x-y)^2(x+y)+(x-y)^3
C=8(x/2 +y)3-6(x+2y)2x+12(x+2y)x2-8x3
D=(x-y)3-(3(x-y)2/2)y+(3(x-y)/4)y^2-y3/8
\(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y\right)^3+3\cdot\left(x+y\right)^2\cdot\left(x-y\right)+3\cdot\left(x+y\right)\cdot\left(x-y\right)^2+\left(x-y\right)^3\)
\(=\left[\left(x+y\right)+\left(x-y\right)\right]^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3\)
\(=8x^3\)
\(---\)
\(C=8\left(x+2y\right)^3-6\left(x+2y\right)^2x+12\left(x+2y\right)x^2-8x^3\) (sửa đề)
\(=\left[2\left(x+2y\right)\right]^3-3\cdot\left(x+2y\right)^2\cdot2x+3\cdot\left(x+2y\right)\cdot\left(2x\right)^2-\left(2x\right)^3\)
\(=\left[2\left(x+2y\right)-2x\right]^3\)
\(=\left(2x+4y-2x\right)^3\)
\(=\left(4y\right)^3\)
\(=64y^3\)
\(---\)
\(D=\left(x-y\right)^3-3\cdot\dfrac{\left(x-y\right)^2}{2}\cdot y+3\cdot\dfrac{\left(x-y\right)}{4}\cdot y^2-\dfrac{y^3}{8}\)
\(=\left(x-y\right)^3-3\cdot\left(x-y\right)^2\cdot\dfrac{y}{2}+3\cdot\left(x-y\right)\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)
\(=\left[\left(x-y\right)-\dfrac{y}{2}\right]^3\)
\(=\left(x-y-\dfrac{y}{2}\right)^3\)
\(=\left(x-\dfrac{3}{2}y\right)^3\)
#\(Toru\)
Đúng 1
Bình luận (0)
a)[2(x-y)3-7(y-x)2-(y-x)]:(x-y)
b)[3(x-y)5-2(x-y)4+3(x-y)2]:[5(x-y)2 ]
a: =2(x-y)^3/(x-y)-7(x-y)^2/(x-y)+(x-y)/(x-y)
=2(x-y)^2-7(x-y)+1
b: =3(x-y)^5/5(x-y)^2-2(x-y)^4/5(x-y)^2+3(x-y)^2/5(x-y)^2
=3/5(x-y)^3-2/5(x-y)^2+3/5
Đúng 1
Bình luận (0)
\(a,\)
\(\left[2\left(x-y\right)^3-7\left(y-x\right)^2-\left(y-x\right)\right]:\left(x-y\right)\)
\(=\left[2\left(x-y\right)^3-7\left(x-y\right)^2+\left(x-y\right)\right]:\left(x-y\right)\)
\(=\left\{\left(x-y\right)\left[2\left(x-y\right)^2-7\left(x-y\right)+1\right]\right\}:\left(x-y\right)\)
\(=2\left(x-y\right)^2-7\left(x-y\right)+1\)
\(b,\)
\(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:\left[5\left(x-y\right)^2\right]\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
rút gọn rồi tính giá trị của biểu thức với x=1/2 ; y= -3
A= (x+y)^2 + (x-y)^2 + 2.(x+y).(x-y)
B= 3.(x-y)^2 - 2.(x+y)^2 - (x-y).(x+y)
C=(x+y)^3 - (x-y)^3 - (6x^2y +1)
D=(x+y).(x^2 - xy + y^2) - (x+y)^3
\(A=\left(x+y\right)^2+\left(x-y\right)^2+2\left(x+y\right)\left(x-y\right)\)
\(=x^2+2xy+y^2+x^2-2xy+y^2+2\left(x^2-y^2\right)\)
\(=2x^2+2x^2=4x^2\)
Vs x = 1/2 ; y = 3 ⇒ \(A=\frac{1}{4}.4=1\)
\(B=3x^2-6xy+y^2-2x^2-4xy-2y^2-x^2+y^2=-10xy=\frac{1}{2}.3.10=15\)
\(C=x^3+3x^2y+3xy^2+y^2-x^3+3x^2y-3xy^2+y^3-6x^2y-1=2y^2-1=18-1=17\)\(D=x^3+y^3-x^3-3x^2y-3xy^2-y^3=-3x^2y-3xy^2=\frac{1}{4}.9+\frac{1}{2}.27=\frac{9}{4}+\frac{108}{4}=\frac{117}{4}\)Check lại nhé <33 sợ sai lém
Phân tích các đa thức sau thành nhân tử:
a) 2(x -1)^ 3 - 5(x -1)^ 2 - (x - 1);
b) x(y - x)^ 3 - y(x - y)^ 2 + xy(x - y);
c) xy(x + y)- 2x - 2y;
d) x(x + y) ^2 - y(x + y)^ 2 + y^ 2 (x - y).
a: Ta có: \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)\)
\(=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]\)
\(=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)\)
\(=\left(x-1\right)\left(2x^2-9x+6\right)\)
b: Ta có: \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=-x\left(x-y\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]\)
\(=\left(x-y\right)\left[-x^3+2x^2y-xy^2-xy+y^2+xy\right]\)
\(=\left(x-y\right)\left(-x^3+2x^2y-xy^2+y^2\right)\)
Đúng 2
Bình luận (0)
a) \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)=\left(x-1\right)\left(2x^2-9x+6\right)\)
b) \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]=\left(x-y\right)\left(-x^3+2x^2y-xy^2-xy+y^2+xy\right)=\left(x-y\right)\left(-x^3+y^2+2x^2y-xy^2\right)\)
c) \(xy\left(x+y\right)-2x-2y=xy\left(x+y\right)-2\left(x+y\right)=\left(x+y\right)\left(xy-2\right)\)
d) \(x\left(x+y\right)^2-y\left(x+y\right)^2+y^2\left(x-y\right)=\left(x+y\right)^2\left(x-y\right)+y^2\left(x-y\right)=\left(x-y\right)\left(x^2+2xy+y^2+y^2\right)=\left(x-y\right)\left(x^2+2y^2+2xy\right)\)
Đúng 0
Bình luận (0)
\(a.2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)\\ =\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]\\ =\left(x-1\right)\left(2x^2-9x+6\right)\)
Đúng 0
Bình luận (0)