a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:

\(\widehat{B}\) là góc chung, \(\widehat{AHB}=\widehat{BAC}=90^o\)

=> \(\Delta HBA~\Delta ABC\) (g.g) (1)

b) Xét \(\Delta HAC\) và \(\Delta ABC\) có:

\(\widehat{C}\) là góc chung, \(\widehat{AHC}=\widehat{BAC}=90^o\)

=> \(\Delta HAC~\Delta ABC\) (g.g) (2)

Từ (1) và (2) suy ra \(\Delta HBA~\Delta HAC\)

=> \(\frac{S_{\Delta HBA}}{S_{\Delta HAC}}=\left(\frac{AB}{AC}\right)^2=\left(\frac{12}{16}\right)^2=\left(\frac{3}{4}\right)^2=\frac{9}{16}\)

Giúp mình với mọi người 😭😭

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC∼ΔHBA(g-g)

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=12^2+16^2=400\)

hay BC=20(cm)

Vậy: BC=20cm

a)  Xét   \(\Delta HBA\) và    \(\Delta ABC\)  có:

\(\widehat{AHB}=\widehat{CAB}=90^0\)

\(\widehat{ABC}\)    CHỤNG

suy ra:     \(\Delta HBA~\Delta ABC\)

b)   Áp dụng định lý Pytago vào tam giác vuông  ABC  ta có:

          \(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\)\(BC^2=12^2+16^2=400\)

\(\Leftrightarrow\)\(BC=\sqrt{400}=20\)cm

     Áp dụng hệ thức lượng trong tam giác vuông ta có:

            \(AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6\)

           \(BH=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\)

@@ câu c sao bạn?

Câu a b dễ r chủ yếu câu c

Bài 5: 

Ta có: \(AB^2=BH\cdot BC\)

\(\Leftrightarrow BH\left(BH+9\right)=400\)

\(\Leftrightarrow BH^2+25HB-16HB-400=0\)

\(\Leftrightarrow BH=16\left(cm\right)\)

hay BC=25(cm)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

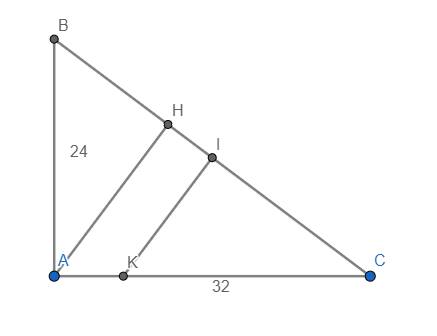
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\)) 

Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)

Nên \(\widehat{HAC}\approx53,13^o\)

Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm

\(\Rightarrow IB=IC=20cm\)

Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\) 

\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)

Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)

Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)

\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)

Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)

Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)

\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHAB đồng dạng với ΔACB

b:  BD/CD=AB/AC=3/4

=>S ABD/S ACD=3/4

c: BC=căn 12^2+16^2=20cm

BD/3=CD/4=20/7

=>BD=60/7cm

AH=12*16/20=9,6cm

Giải nhanh giúp mình với

Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=7,5\left(cm\right)\)

Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)

Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\\BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)

Áp dụng PTG: \(HM=\sqrt{AM^2-AH^2}=2,1\left(cm\right)\)

Vậy \(S_{AHM}=\dfrac{1}{2}HM\cdot AH=\dfrac{1}{2}\cdot2,1\cdot7,2=7,56\left(cm^2\right)\)

Ai sẽ giúp m chứ??

a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHBA đồng dạng vơi ΔABC

b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)

BH=12^2/20=7,2cm

c: \(S_{ABC}=\dfrac{1}{2}\cdot12\cdot16=6\cdot16=96\left(cm^2\right)\)

a) xét△HBA và △ABC có:

góc BAH= góc BHA (=90 độ)

góc B chung

⇒△HBA∼△ABC (g.g)

b) áp dụng định lí pytago vào △ABC vuông tại A

AB²+AC²=BC²

⇔16²+12²=BC²

⇔256+144=BC²

⇔√400=20=BC(cm)

vậy BC= 20 cm

vì△HBA∼△ABC(cmt)

ta có tỉ lệ

\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\)hay \(\dfrac{AH}{16}=\dfrac{12}{20}\)

⇒\(AH=\dfrac{12\cdot16}{20}=\dfrac{48}{5}=9.6\left(cm\right)\)

⇒AH = 9,6 cm

áp dụng tính chất đường phân giácAD trong tam giác

\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)⇒\(\dfrac{12}{16}=\dfrac{BD}{DC}\)⇒\(\dfrac{DC}{16}=\dfrac{BD}{12}\)

áp dụng tính chất của dãy tỉ số bằng nhau ta có

\(\dfrac{DC}{16}=\dfrac{BD}{12}=\dfrac{DC+BD}{28}=\dfrac{20}{28}=\dfrac{5}{7}\)

\(\dfrac{BD}{12}=\dfrac{5}{7}\)⇒\(BD=\dfrac{60}{7}\left(cm\right)\)

c) \(DC=BC-BD=20-\dfrac{60}{7}=\dfrac{80}{7}\)

hs tự làm

Học Hành Con Cặk Vào Game mẹ đi hc cc

Hc hành cái củ cak vào game mẹ đi chăm hc cái cc