Chứng minh : BC2 = AB2+AC2 - 2.AB.AC . cosA

Những câu hỏi liên quan
Cho tam giác ABC có ∠A = 60 0 Chứng minh rằng:
B C 2 = A B 2 + A C 2 - AB.AC
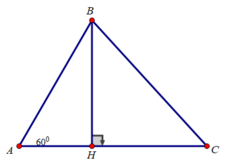
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
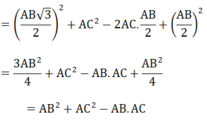
Vậy được điều phải chứng minh.
Đúng 0
Bình luận (0)
Cho tam giác ABC có
∠
A
60
°
. Chứng minh rằng:
B
C
2
A
B
2
+
A
C
2
-
A
B
....
Đọc tiếp
Cho tam giác ABC có ∠ A = 60 ° . Chứng minh rằng: B C 2 = A B 2 + A C 2 - A B . A C
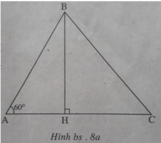
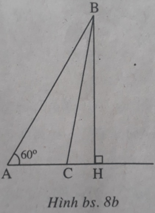
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C
Đúng 0
Bình luận (0)
Câu 20: Tam giác ABC vuông tại B suy ra: A. AC2 AB2 + BC2 B. AC2 AB2 - BC2 C. BC2 AB2 + AC2 D. AB2 BC2 + AC2Câu 21: Tam giác ABC có BC 5cm; AC 12cm; AB 13cm. Tam giác ABC vuông tại đâu? A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuôngCâu 22: Cho ABC có 900 ; AB 4,5 cm ; BC 7,5 cm...
Đọc tiếp
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
Ai giúp mình với ạ!
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
Đúng 1
Bình luận (0)
10. Cho ![]() vuông tại B chọn câu đúng
vuông tại B chọn câu đúng
a.BC2 = AB2 + AC2 b. AB2 = AC2 + BC2 c. AC2 = BC2 + AB2
Cho tam giác ABC, đường cao AH. Chứng minh: AB2+AC2=BC2
Cho tam giác cân ABC (AB = AC), đường cao CD (D ở giữa A và B).
Chứng minh rằng: AB2 + BC2 + AC2 = BD2 + 2AD2 + 3DC2
Cho hình bình hành ABCD. CM: AB2 + BC2 + CD2 +DA2 = AC2 +BD2
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
Đúng 0
Bình luận (0)
cho tam giác ABC . M là trung điểm BC . c m AB2 AC2 2 AM2 BC2 2
Cho tứ diện ABCD có trọng tâm G. Chứng minh AB2 + AC2 + AD2 + BC2 + BD2 + CD2 = 4(GA2 + GB2 + GC2 + GD2)
Cho tam giác ABC, góc A < 90o, M là trung điểm của BC. CMR:
AB2 + AC2 = 2AM2 + BC2/2
Tham Khảo e nhá chj ngu ném ko bik làm☹
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-m-la-trung-diem-bc-chung-minh-ab2-ac2-2am2-bc22.249563555147
Đúng 0
Bình luận (0)
Kẻ AH vuông góc BC.
Xét tam giác AHM vuông tại H (^AHM = 900) có:
AM2 = AH2 + HM2 (định lý Pytago).
Xét tam giác AHB vuông tại H (^AHB = 900) có:
AB2 = AH2 + BH2 (định lý Pytago).
Xét tam giác AHC vuông tại H (^AHC = 900) có:
AC2 = AH2 + CH2 (định lý Pytago).
Ta có: BH = BM - HM.
CH = CM + HM.
Vì M là trung điểm của BC (gt) => BM = CM; BM = \(\dfrac{BC}{2}\) => BM2 = \(\dfrac{BC^2}{4}\).
Ta có: AB2 + AC2 = AH2 + BH2 + AH2 + CH2.
AB2 + AC2 = AH2 + AH2 + BH2 + CH2.
= 2AH2 + (BM - HM)2 + (CM + HM)2.
= 2AH2 + BM2 - 2BM.HM + HM2 + CM2 + 2CM.HM + HM2.
= 2AH2 + BM2 - 2BM.HM + HM2 + BM2 + 2BM.HM + HM2.
= 2AH2 + 2HM2 + 2BM2.
= 2(AH2 + HM2) + 2\(\dfrac{BC^2}{4}\).
AB2 + AC2 = 2AM2 + \(\dfrac{BC^2}{2}\) (đpcm).
Đúng 1
Bình luận (0)
























