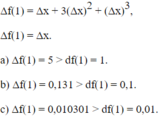1, So sánh A và B biết A=\(\dfrac{2^{19}.27^3+15.4^9.9^4}{6^9.2^{10}+12^{10}}\) B=\(\dfrac{4}{35}+\dfrac{4}{63}+\dfrac{4}{99}+\dfrac{4}{143}+\dfrac{4}{195}\) ( GIÚP Mk Với Mk Đang Cần Gấp )

Những câu hỏi liên quan
Bài 1:Chứng tỏ các đa thức sau ko có nghiệm.
a) x²+x+2
b) x²+x+1
Bài 2: Cho tam giác ABC cân tại A. Trên tia đối của tia CB lấy điểm D.
a) So sánh AD và AB
b) Vẽ BE vuông góc với AC và DF vuông góc với AB. So sánh BF và DF
Ta có
\(x^2+x+1=\left(x+\frac{1}{2}\right)+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy x^2+x+1 k có nghiệm
Ta có
\(x^2+x+1>0\)
\(\Rightarrow x^2+x+2>0\)
Vậy....
Bài 1:
a) Biến đổi \(f\left(x\right)\), ta có:
\(f\left(x\right)=x^2+x+2\)
\(=x^2+\frac{1}{2}x+\frac{1}{2}x+\frac{1}{4}+\frac{7}{4}\)
\(=x\left(x+\frac{1}{2}\right)+\frac{1}{2}\left(x+\frac{1}{2}\right)+\frac{7}{4}\)
\(=\left(x+\frac{1}{2}\right)\left(x+\frac{1}{2}\right)+\frac{7}{4}\)
\(=\left(x+\frac{1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)
\(\Rightarrow\forall x\) ta có \(f\left(x\right)\ne0\)
Vậy \(f\left(x\right)\) không có nghiệm
b) Tương tự
a) Kẻ \(AH\perp BC\) tại \(H\)
Ta có:
\(AB=AC\)
\(\Rightarrow HB=HC\)
Lại có:
\(D\in\) tia đối của tia \(CB\)
Vậy nên \(HD>HC=HB\)
\(\Rightarrow AD>AB\)
b) \(S_{\Delta ABC}=\frac{1}{2}AH.BC\)
\(S_{\Delta ABD}=\frac{1}{2}AH.BD\)
Mà \(BC< BD\)
\(\Rightarrow S_{\Delta ABC}< S_{\Delta ABD}\)
Lại có:
\(S_{\Delta ABC}=\frac{1}{2}AC.BE\)
\(S_{\Delta ABD}=\frac{1}{2}AB.DF\)
\(\Rightarrow\frac{1}{2}AC.BE< \frac{1}{2}AB.DF\)
\(\Rightarrow BE< DE\left(đpcm\right)\)
cho tam giác ABC cân tại A.trên tia đối của tia CB lấy điểm D. a) so sánh AD và AB ; b)vẽ BE vuông góc AC và DF vuông góc AB.so sánh BE và DF
a: Xét ΔACD có \(\widehat{ACD}\) là góc tù
nên AD là cạnh lớn nhất
Suy ra: AD>AC
hay AD>AB
Đúng 0
Bình luận (0)
:
Cho tam giác ABC cân tại A . Trên tia đối của tia CB lấy điểm D
a/ So sánh AD và AB
b/ Vẽ BE vuông góc với AC tại E và DF vuông góc với AB tại F. So sánh BE và
DF
Cho hàm số
f ( x ) = x 3 − 2 x + 1 .
Hãy tính Δf(1), df(1) và so sánh chúng, nếu
a) Δx = 1;
b) Δx = 0,1;
c) Δx = 0,01;
Đề ôn tập HK 2 - Đề 8 Bài 1:a) Biết -3a - 1 -3b - 1. So sánh a và b?b) Biết 4a + 3 4b + 3. So sánh a và b?Bài 2: Biết a b, hãy so sánh:a) 3a - 7 và 3b - 7. b) 5 - 2a và 3 - 2bc) 2a + 3 và 2b + 3. d) 3a - 4 và 3b - 3Bài 3: a) Chứng minh pt: x² + 6x + 11 0 vô nghiệm b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số nghiệm.
Đọc tiếp
Đề ôn tập HK 2 - Đề 8
Bài 1:
a) Biết -3a - 1 > -3b - 1. So sánh a và b?
b) Biết 4a + 3 < 4b + 3. So sánh a và b?
Bài 2: Biết a < b, hãy so sánh:
a) 3a - 7 và 3b - 7. b) 5 - 2a và 3 - 2b
c) 2a + 3 và 2b + 3. d) 3a - 4 và 3b - 3
Bài 3: a) Chứng minh pt: x² + 6x + 11 = 0 vô nghiệm
b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số nghiệm.
1.
a. -3a - 1 + 1 > -3b - 1 + 1 (cộng cả 2 vế cho 1)
-3a . \(\left(\dfrac{-1}{3}\right)\) < -3b . \(\left(\dfrac{-1}{3}\right)\) (nhân cả vế cho \(\dfrac{-1}{3}\) )
a < b
b. 4a + 3 + (- 3) < 4b + 3 +(- 3) (cộng cả 2 vế cho -3)
4a . \(\dfrac{1}{4}\) < 4b . \(\dfrac{1}{4}\) (nhân cả 2 vế cho \(\dfrac{1}{4}\) )
a < b
2.
a. Ta có: a < b
3a < 3b ( nhân cả 2 vế cho 3)
3a - 7 < 3b - 7 (cộng cả 2 vế cho - 7 )
b. Ta có: a < b
-2a > -2b (nhân cả 2 vế cho -2)
5 - 2a > 5 - 2b ( cộng cẩ 2 vế cho 5)
c. Ta có: a < b
2a < 2b (nhân cả vế cho 2)
2a + 3 < 2b + 3 (cộng cả 2 vế cho 3)
d. Ta có: a < b
3a < 3b (nhân cả 2 vế cho 3)
3a - 4 < 3b - 4 (cộng cả 2 vế cho -4)
Ta có: 3 < 4
đến đây ko bắt cầu qua đc chắc đề bài sai
Đúng 1
Bình luận (0)
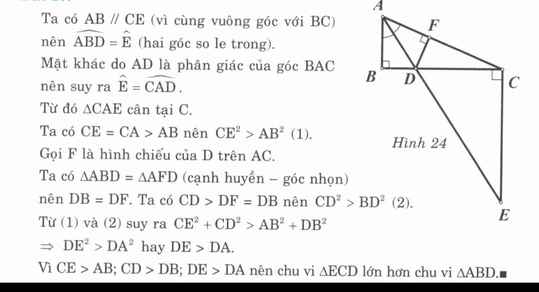
Bài 10. Cho tam giác ABC vuông tại B, AD là phân giác của góc A. Từ C kẻ đường vuông góc với BC, cắt
AD kéo dài tại E.
a) Chứng minh AC = CE và so sánh CE với AB.
b) Kẻ DF ⊥ AC . Chứng minh DF = DB và DC > DB
c) So sánh chu vi của tam giác ECD và tam giác ABD.
a: Xét ΔACE có \(\widehat{CAE}=\widehat{CEA}\left(=\widehat{BAD}\right)\)
nên ΔACE cân tại C
hay CA=CE
=>CE>AB
b: Xét ΔABD vuông tại B và ΔAFD vuông tại F có
AD chung
\(\widehat{BAD}=\widehat{FAD}\)
Do đó: ΔABD=ΔAFD
Suy ra: DB=DF
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A.Trên tia đối của tia CB lấy điểm D.
a,So sánh AD và AB .
b,Vẽ BE vuông góc AC;DF vuông góc AB.So sánh BE và DF.
nhanh lên giúp mình nha~~
Cho tam giác DEF có DE<DF .Vẽ đường cao DH
a,so sánh HE và HF
b,lấy điểm M trên DH,so sánh ME và MF
c,so sánh góc HDE và góc HDF
MỌI NGƯỜI GIÚP MÌNH NHA!
Khó vãi!!! Nghỉ ở nhà bây giờ ko nhớ tí kiến thức gì lun!!! Chắc phải mơ sách giáo khoa ra rùi tự nghiên cứu lại thui!!!
B. Phần tự luận (7 điểm)
Cho tam giác DEF có DE < DF. Đường cao DH
a. So sánh HE và HF
a. Vì DE < DF ⇒ HE < HF(quan hệ giữa hình chiếu và đường xiên) (1 điểm)
Đúng 0
Bình luận (0)
a ) so sánh c và d biết : C dfrac{1957}{2007} với D dfrac{1935}{1985}b )hãy so sánh A và Bcho A dfrac{2016^{2016}+2}{2016^{2016}-1} và B dfrac{2016^{2016}}{2016^{2016}-3}c ) so sánh M và N biết :M dfrac{10^{2018}+1}{10^{2019}+1} ; N dfrac{10^{2019}+1}{10^{2020}+1}
Đọc tiếp
a ) so sánh c và d biết :
C = \(\dfrac{1957}{2007}\) với D = \(\dfrac{1935}{1985}\)
b )hãy so sánh A và B
cho A = \(\dfrac{2016^{2016}+2}{2016^{2016}-1}\) và B = \(\dfrac{2016^{2016}}{2016^{2016}-3}\)
c ) so sánh M và N biết :
M = \(\dfrac{10^{2018}+1}{10^{2019}+1}\) ; N = \(\dfrac{10^{2019}+1}{10^{2020}+1}\)
Giải:
a)Ta có:
C=1957/2007=1957+50-50/2007
=2007-50/2007
=2007/2007-50/2007
=1-50/2007
D=1935/1985=1935+50-50/1985
=1985-50/1985
=1985/1985-50/1985
=1-50/1985
Vì 50/2007<50/1985 nên -50/2007>-50/1985
⇒C>D
b)Ta có:
A=20162016+2/20162016-1
A=20162016-1+3/20162016-1
A=20162016-1/20162016-1+3/20162016-1
A=1+3/20162016-1
Tương tự: B=20162016/20162016-3
B=1+3/20162016-3
Vì 20162016-1>20162016-3 nên 3/20162016-1<3/20162016-3
⇒A<B
Chúc bạn học tốt!
Đúng 1
Bình luận (0)
Làm tiếp:
c)Ta có:
M=102018+1/102019+1
10M=10.(102018+1)/202019+1
10M=102019+10/102019+1
10M=102019+1+9/102019+1
10M=102019+1/102019+1 + 9/102019+1
10M=1+9/102019+1
Tương tự:
N=102019+1/102020+1
10N=1+9/102020+1
Vì 9/102019+1>9/102020+1 nên 10M>10N
⇒M>N
Chúc bạn học tốt!
Đúng 0
Bình luận (0)